题目内容
6.若a,b是正实数,且a+b=2,则$\frac{1}{1+a}+\frac{1}{1+b}$的最小值是1.分析 由题意可得(1+a)+(1+b)=4,代入可得$\frac{1}{1+a}+\frac{1}{1+b}$=$\frac{1}{4}$($\frac{1}{1+a}+\frac{1}{1+b}$)[(1+a)+(1+b)]=$\frac{1}{4}$(2+$\frac{1+b}{1+a}$+$\frac{1+a}{1+b}$),由基本不等式可得.
解答 解:∵a,b是正实数,且a+b=2,
∴(1+a)+(1+b)=4,
∴$\frac{1}{1+a}+\frac{1}{1+b}$=$\frac{1}{4}$($\frac{1}{1+a}+\frac{1}{1+b}$)[(1+a)+(1+b)]
=$\frac{1}{4}$(2+$\frac{1+b}{1+a}$+$\frac{1+a}{1+b}$)≥$\frac{1}{4}$(2+2$\sqrt{\frac{1+b}{1+a}•\frac{1+a}{1+b}}$)=1
当且仅当$\frac{1+b}{1+a}$=$\frac{1+a}{1+b}$即a=b=1时取等号,
故答案为:1.
点评 本题考查基本不等式求最值,凑出可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.设随机变量X的概率分布列为
则E(X+2)的值为( )
| X | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{2}$ |
| A. | $\frac{11}{3}$ | B. | 9 | C. | $\frac{13}{3}$ | D. | $\frac{7}{3}$ |
14.阅读如图所示程序框图,运行相应的程序,则输出的结果是( )
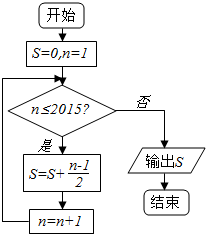

| A. | $\frac{2015×2016}{4}$ | B. | $\frac{2014×2015}{4}$ | C. | $\frac{2015×2016}{2}$ | D. | $\frac{2014×2015}{2}$ |
1.已知集合U={x|x≤-1或x≥0},A={x|0≤x≤2},B={x|x2>1},则集合A∩(∁UB)等于( )
| A. | {x|x>0或x<-1} | B. | {x|1<x≤2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
18.已知α是第二象限角,tanα=-$\frac{8}{15}$,则sinα=( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{8}{17}$ | D. | $-\frac{8}{17}$ |