题目内容
设u,v∈R，且|u|≤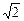
,v＞0,则(u－v)2+(
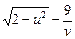)2的最小值为( )
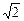,v＞0,则(u－v)2+(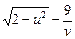)2的最小值为( )| A．4 | B．2 | C．8 | D．2 |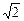
C
考虑式子的几何意义，转化为求圆x2+y2=2上的点与双曲线xy=9上的点的距离的最小值
练习册系列答案
冲刺100分1号卷系列答案
期末好成绩系列答案
相关题目
冲刺100分1号卷系列答案期末好成绩系列答案题目内容
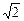,v＞0,则(u－v)2+(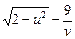)2的最小值为( )| A．4 | B．2 | C．8 | D．2 |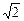
冲刺100分1号卷系列答案期末好成绩系列答案
到
，
距离之差为
，到
轴，
轴距离之比为
，求
的取值范围．
，试讨论当
的值变化时，方程
表示的曲线形状.
,点P为线段MN的中点。 
与上述轨迹交于A.B两点，且
,求：
的焦点与双曲线
的右焦点重合，则
的值为 ．
上横坐标为4的点到焦点的距离为5.
与抛物线C交于两点
，
，且
（
，且
为常数）.过弦AB的中点M作平行于
轴的直线交抛物线于点D，连结AD、 BD得到
.
；
0
的离心率为
，右准线
与两渐近线交于Ｐ，Ｑ两点，其右焦点为Ｆ，且△PQF为等边三角形。
截得弦长为
，求双曲线方程；
，以F为左焦点，为