题目内容

已知：2x≤256且log2x，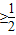
（1）求x的取值范围；
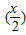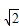
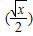（2）求函数f（x）=log2•log的最大值和最小值．
【答案】分析：（1）利用指数与对数不等式求出x的范围，求出交集即可．
（2）通过x的范围求出log2x的范围，化简函数表达式，通过二次函数的最值求出函数的最值即可．
解答：解：（1）由2x≤256得x≤8，log2x得x≥，∴．
（2）由（1）得，
f（x）=log2•log=（log2x-log22）（lo）
∴f（x）=（log2x-1）（log2x-2）=（log2x-）2-，
当log2x=，f（x）min=-．
当log2x=3，f（x）max=2．
点评：本题考查指数与对数不等式的解法，函数的最值的求法，考查转化思想，计算能力．
练习册系列答案
相关题目
已知：2x≤256且log2x≥
1
2
，
（1）求x的取值范围；
（2）求函数f（x）=log2 (
x
2
)•log 
2
 (
x
2
)的最大值和最小值．
已知：2x≤256且log2x≥
1
2
，
（1）求x的取值范围；
（2）求函数f(x)=log2(
x
2
)•log2(
x
4
)的最大值和最小值及对应的x值．
已知：2x≤256且log2x≥
1
2
．
（1）求x的取值范围；
（2）将函数f（x）=log2（
x
2
）•log 
2
（
x
2
）的解析式整理为关于log2x的式子；
（3）在前两问的情形下求函数f（x）的最大值和最小值．
已知：2x≤256且log2x≥
1
2
，
（1）求x的取值范围；
（2）求函数f（x）=log2 (
x
2
)•log 
2
 (
x
2
)的最大值和最小值．
已知：2x≤256且log2x，
（1）求x的取值范围；
（2）求函数f（x）=log2•log的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网