题目内容
已知一次函数y=f(x)的图象关于直线y=x对称的图象为C,且f(1)=0,若点A(n ,
)(n∈N*)在C上,a1=1,当n≥2时,
-
=1
(1)求数列{an}的通项公式;
(2)设Sn=
+
+
+…+
,求
Sn.
| an+1 |
| an |
| an+1 |
| an |
| an |
| an-1 |
(1)求数列{an}的通项公式;
(2)设Sn=
| a1 |
| 3! |
| a2 |
| 4! |
| a3 |
| 5! |
| an |
| (n+2)! |
| lim |
| n→∞ |
分析:(1)依题意C过点(0,1),所以设C方程为y=kx+1,由条件推出k=1,
=n+1,从而推出
=n,
=n-1,…,
=2,且a1=1,各式相乘得an的解析式.
(2)化简Sn中的通项为
-
,代入Sn 的表达式化简为
-
,从而求出
Sn的值.
| an+1 |
| an |
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
(2)化简Sn中的通项为
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| lim |
| n→∞ |
解答:解:(1)依题意C过点(0,1),所以设C方程为y=kx+1.
因为点A(n ,
)(n∈N*)在C上,所以
=kn+1,
代入
-
=1,得k=1,故
=n+1.
∴
=n,
=n-1,…,
=2,且a1=1,
各式相乘得an=n!.
(2)∵
=
=
=
-
,
∴Sn=
-
+
-
+…+
-
=
-
,
∴
Sn=
.
因为点A(n ,
| an+1 |
| an |
| an+1 |
| an |
代入
| an+1 |
| an |
| an |
| an-1 |
| an+1 |
| an |
∴
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
各式相乘得an=n!.
(2)∵
| an |
| (n+2)! |
| n! |
| (n+2)! |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
∴
| lim |
| n→∞ |
| 1 |
| 2 |
点评:本题主要考查利用数列的递推关系求数列的通项公式,用裂项法进行数列求和,求数列的极限,属于中档题.

练习册系列答案
相关题目
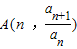 (n∈N*)在C上,a1=1,当n≥2时,
(n∈N*)在C上,a1=1,当n≥2时,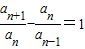
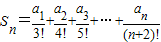 ,求
,求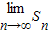 .
.