题目内容
5.已知函数f(x)=x3+bx2+cx+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.(1)求函数y=f(x)的解析式;
(2)求函数g(x)=$\frac{3}{2}{x^2}$-9x+a+2与y=f(x)的图象有三个交点,求a的范围.
分析 (1)由图象过点P(0,2)求出d的值,再代入求出导数,再由切线方程求出f(-1)、f′(-1),分别代入求出b和c的值;
(2)将条件转化为x3-$\frac{9}{2}$x2+6x=a有三个根,再转化为h(x)=x3-$\frac{9}{2}$x2+6x的图象与y=a图象有三个交点,再求出h(x)的导数、临界点、单调区间和极值,再求出a的范围即可.
解答 解:(1)由f(x)的图象经过点P(0,2),得d=2.
∴f′(x)=3x2+2bx+c,
由在M(-1,f(-1))处的切线方程是6x-y+7=0,
∴-6-f(-1)+7=0,得f(-1)=1,且f′(-1)=6.
∴$\left\{\begin{array}{l}{3-2b+c=6}\\{-1+b-c+2=1}\end{array}\right.$,即$\left\{\begin{array}{l}{2b-c=-3}\\{b=c}\end{array}\right.$,解得b=c=-3.
故所求的解析式是f(x)=x3-3x2-3x+2;
(2)∵函数g(x)与f(x)的图象有三个交点,
∴方程x3-3x2-3x+2=$\frac{3}{2}$x2-9x+a+2有三个根,
即x3-$\frac{9}{2}$x2+6x=a有三个根,
令h(x)=x3-$\frac{9}{2}$x2+6x,则h(x)的图象与y=a图象有三个交点.
接下来求h(x)的极大值与极小值,
∴h′(x)=3x2-9x+6,令h′(x)=0,解得x=1或2,
当x<1或x>2时,h′(x)>0;当1<x<2时,h′(x)<0,
∴h(x)的增区间是(-∞,1),(2,+∞);减区间是(1,2),
∴h(x)的极大值为h(1)=$\frac{5}{2}$,h(x)的极小值为h(2)=2
因此2<a<$\frac{5}{2}$.
点评 本题导数的几何意义、切点坐标的应用,导数研究函数的性质:单调性和极值等,涉及了函数图象的交点与方程之间的转化问题,待定系数法求解析式

| A. | 4 | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | 1 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
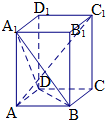 在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,给出下列结论:
在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,给出下列结论: