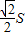题目内容
已知圆锥的侧面展开图为半圆,半圆的面积为S,则圆锥的底面面积是( )
| A、2S | ||||
B、
| ||||
C、
| ||||
D、
|
分析:由已知中圆锥的侧面展开图为半圆且面积为S,我们易确定圆锥的母线长L与底面半径R之间的关系,进而求出底面面积即可得到结论.
解答:解:设圆锥的母线长为L,底面半径为R
若圆锥的侧面展开图为半圆则:
2πR=πL
即L=2R
又∵圆锥的侧面展开图为半圆且面积为S,
则圆锥的底面面积是
故选B.
若圆锥的侧面展开图为半圆则:
2πR=πL
即L=2R
又∵圆锥的侧面展开图为半圆且面积为S,
则圆锥的底面面积是
| S |
| 2 |
故选B.
点评:本题考查的知识点是圆锥的表面积,其中根据已知中圆锥的侧面展开图为半圆,确定圆锥的母线长与底面半径的关系是解答本题的关键.

练习册系列答案
相关题目
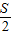
 S
S