题目内容
设函数f(x)=px- -2lnx,且f(e)=pe-
-2lnx,且f(e)=pe- -2,(其中e=2.1828…是自然对数的底数).
-2,(其中e=2.1828…是自然对数的底数).(1)求p与q的关系;
(2)若f(x)在其定义域内为单调函数,求p的取值范围;
(3)设
 ,若在[1,e]上存在实数x,使得f(x)>g(x)成立,求实数p的取值范围.
,若在[1,e]上存在实数x,使得f(x)>g(x)成立,求实数p的取值范围.
【答案】分析:(1)由题意f(x)=px-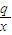 -2lnx,且f(e)=pe-
-2lnx,且f(e)=pe-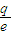 -2,将其移项通分就可以看出来了;
-2,将其移项通分就可以看出来了;
(2)首先求出函数的导数f′(x),因为f(x)在其定义域内为单调函数,说明导数恒大于或小于0,从而求出p的取值范围;
(3)先假设存在,因为设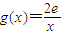 ,若在[1,e]上存在实数x,使得f(x)>g(x),在区间[1,e]上分别求出f(x)和g(x)的最大值和最小值,然后讨论求解.
,若在[1,e]上存在实数x,使得f(x)>g(x),在区间[1,e]上分别求出f(x)和g(x)的最大值和最小值,然后讨论求解.
解答:解:(1)∵f(e)=pe- -2,
-2,
∴(p-q)e=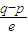 ,∴p-q=0,
,∴p-q=0,
∴p=q;
(2)f′(x)=p+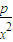 -
-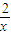 ≥0,或f′(x)≤0在(0,+∞)恒成立,
≥0,或f′(x)≤0在(0,+∞)恒成立,
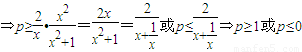 ;
;
(3)∵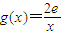 在[1,e]上是减函数
在[1,e]上是减函数
∴x=e时,g(x)min=2;
x=1时,g(x)max=2e,
即g(x)∈[2,2e]
①p≤0时,由(2)知f(x)在[1,e]递减⇒fmax(x)=f(1)=0<2,不合题意

∴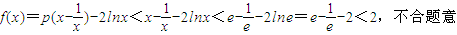
③p≥1时,由(2)知f(x)在[1,e]上是增函数,故只需f(x)max>g(x)min=2,
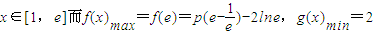
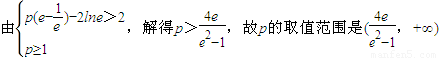 .
.
点评:此题主要考查对数函数的导数,函数单调性的判定,函数最值,函数、方程与不等式等基础知识,一般出题者喜欢考查学生的运算求解能力、推理论证能力及分析与解决问题的能力,要出学生会用数形结合的思想、分类与整合思想,化归与转化思想、有限与无限的思想来解决问题.
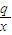 -2lnx,且f(e)=pe-
-2lnx,且f(e)=pe-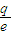 -2,将其移项通分就可以看出来了;
-2,将其移项通分就可以看出来了;(2)首先求出函数的导数f′(x),因为f(x)在其定义域内为单调函数,说明导数恒大于或小于0,从而求出p的取值范围;
(3)先假设存在,因为设
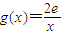 ,若在[1,e]上存在实数x,使得f(x)>g(x),在区间[1,e]上分别求出f(x)和g(x)的最大值和最小值,然后讨论求解.
,若在[1,e]上存在实数x,使得f(x)>g(x),在区间[1,e]上分别求出f(x)和g(x)的最大值和最小值,然后讨论求解.解答:解:(1)∵f(e)=pe-
 -2,
-2,∴(p-q)e=
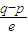 ,∴p-q=0,
,∴p-q=0,∴p=q;
(2)f′(x)=p+
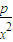 -
-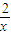 ≥0,或f′(x)≤0在(0,+∞)恒成立,
≥0,或f′(x)≤0在(0,+∞)恒成立,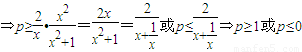 ;
;(3)∵
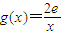 在[1,e]上是减函数
在[1,e]上是减函数∴x=e时,g(x)min=2;
x=1时,g(x)max=2e,
即g(x)∈[2,2e]
①p≤0时,由(2)知f(x)在[1,e]递减⇒fmax(x)=f(1)=0<2,不合题意

∴
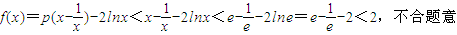
③p≥1时,由(2)知f(x)在[1,e]上是增函数,故只需f(x)max>g(x)min=2,
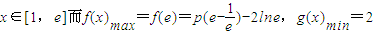
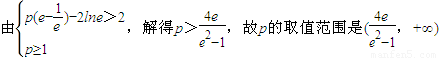 .
.点评:此题主要考查对数函数的导数,函数单调性的判定,函数最值,函数、方程与不等式等基础知识,一般出题者喜欢考查学生的运算求解能力、推理论证能力及分析与解决问题的能力,要出学生会用数形结合的思想、分类与整合思想,化归与转化思想、有限与无限的思想来解决问题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目