Question

14、设函数f（x）的定义域为D，若存在非零实数t使得对于任意x∈M（M⊆D），有x+t∈D，且f（x+t）≥f（x），则称f（x）为M上的t高调函数．如果定义域为[-1，+∞）的函数f（x）=x²为[-1，+∞）上的m高调函数，那么实数m的取值范围是

m≥2

．如果定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x-a²|-a²，且f（x）为R上的4高调函数，那么实数a的取值范围是

-1≤a≤1

．

Answer 1

分析：根据“存在非零实数t使得对于任意x∈M（M⊆D），有x+t∈D，且f（x+t）≥f（x），则称f（x）为M上的t高调函数”的定义，对于定义域为[-1，+∞）的函数f（x）=x²为m高调函数，易知f（-1）=f（1），故得m≥1-（-1），即m≥2；定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x-a²|-a²，画出函数图象，可得4≥3a²-（-a²）?-1≤a≤1．

解答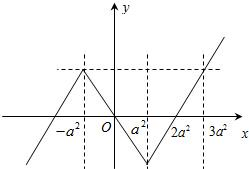：解：∵f（-1）=f（1），m≥1-（-1），即m≥2，
f（x）=|x-a²|-a²的图象如图，∴4≥3a²-（-a²）?-1≤a≤1．
故答案为：m≥2；-1≤a≤1

点评：考查学生的阅读能力，很应用知识分析解决问题的能力，考查数形结合的能力，用图解决问题的能力，属中档题．