题目内容
若不等式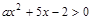 的解集是
的解集是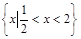 ,
,
(1) 求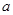 的值;
的值;
(2) 求不等式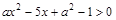 的解集.
的解集.
(1)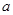 =-2 (2)
=-2 (2)
解析试题分析:(1)依题意,可知方程 的两个实数根为
的两个实数根为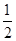 和2, 2分
和2, 2分
由韦达定理得: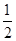 +2=
+2= 4分
4分
解得: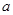 =-2 5分
=-2 5分
(2)不等式 化为
化为 ,∴
,∴ ,
,
故原不等式的解集为 10分
10分
考点:本题考查了一元二次不等式的解法
点评:一元二次不等式的解法的考查主要有:一是利用一元二次不等式与相应的二次函数、一元二次方程的联系解一元二次不等式的出题;二是求含参数的一元二次不等式的解集或者利用不等式求参数范围,一般要对参数进行分类讨论

练习册系列答案
相关题目
若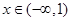 ,则函数
,则函数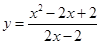 有( )
有( )
| A.最小值1 | B.最大值1 | C.最大值 | D.最小值 |
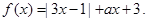
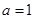 ,解不等式
,解不等式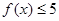 ;
;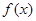 有最小值,求实数
有最小值,求实数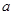 的取值范围.
的取值范围.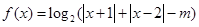 .
.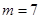 时,求函数
时,求函数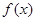 的定义域;
的定义域; 的不等式
的不等式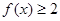 的解集是R,求
的解集是R,求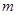 的取值范围.
的取值范围. 是实数,试解关于
是实数,试解关于 的不等式:
的不等式:
 ,不等式
,不等式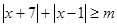 恒成立.
恒成立.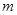 的取值范围;
的取值范围;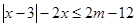 .
.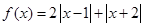 (1)求不等式
(1)求不等式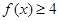 的解集;
的解集;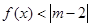 的解集是非空集合,求实数m的取值范围.
的解集是非空集合,求实数m的取值范围.
 且
且 ,求
,求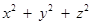 的最小值.
的最小值.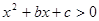 的解集为
的解集为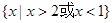
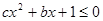 的解集.
的解集.