题目内容
 (2013•海口二模)如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
(2013•海口二模)如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.(Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求异面直线BS与AC所成角的大小.
分析:(I)由等边三角形三线合一,可得SO⊥BC,由勾股定理可得OA⊥SO,结合线面垂直的判定定理得到SO⊥平面ABC;
(Ⅱ)分别取AB、SC、OC的中点N、M、H,连MN、OM、ON、HN、HM,由三角形中位线定理及异面直线夹角的定义,可得OM、ON所成角即为异面直线BS与AC所成角,解三角形MON可得答案.
(Ⅱ)分别取AB、SC、OC的中点N、M、H,连MN、OM、ON、HN、HM,由三角形中位线定理及异面直线夹角的定义,可得OM、ON所成角即为异面直线BS与AC所成角,解三角形MON可得答案.
解答: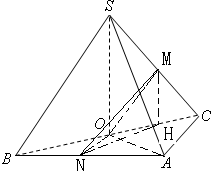 证明:(Ⅰ)因为侧面SAB与侧面SAC均为等边三角形,所以SB=SC
证明:(Ⅰ)因为侧面SAB与侧面SAC均为等边三角形,所以SB=SC
又O为BC中点,所以SO⊥BC
连OA,设AB=2,由∠BAC=90°易求得0A=S0=
所以OA2+SO2=SA2,所以OA⊥SO
因为OA,BC是平面ABC内的两条相交直线,所以SO⊥平面ABC.
解:(Ⅱ)分别取AB、SC、OC的中点N、M、H,连MN、OM、ON、HN、HM,
由三角形中位线定理
ON∥AC,ON=
AC,OM∥BS,OM=
BS,HM∥OS,HM=
OS
所以OM、ON所成角即为异面直线BS与AC所成角
设AB=2,易求得
IN=IM=1,MN=
|cos∠MON|=|
|=
所以异面直线BS与AC所成角的大小为
.
 证明:(Ⅰ)因为侧面SAB与侧面SAC均为等边三角形,所以SB=SC
证明:(Ⅰ)因为侧面SAB与侧面SAC均为等边三角形,所以SB=SC又O为BC中点,所以SO⊥BC
连OA,设AB=2,由∠BAC=90°易求得0A=S0=
| 2 |
所以OA2+SO2=SA2,所以OA⊥SO
因为OA,BC是平面ABC内的两条相交直线,所以SO⊥平面ABC.
解:(Ⅱ)分别取AB、SC、OC的中点N、M、H,连MN、OM、ON、HN、HM,
由三角形中位线定理
ON∥AC,ON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以OM、ON所成角即为异面直线BS与AC所成角
设AB=2,易求得
IN=IM=1,MN=
| 3 |
|cos∠MON|=|
| ON2+OM2-MN2 |
| 2•ON•OM |
| 1 |
| 2 |
所以异面直线BS与AC所成角的大小为
| π |
| 3 |
点评:本题考查的知识点是直线与平面垂直的判定,异面直线及其所成的角,其中(I)的关键是熟练掌握线面垂直的判定定理,(II)的关键是确定异面直线的夹角.

练习册系列答案
相关题目
 (2013•海口二模)已知集合M={-1,0,1},N={0,1,2},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•海口二模)已知集合M={-1,0,1},N={0,1,2},则如图所示韦恩图中的阴影部分所表示的集合为( ) (2013•海口二模)设偶函数f(x)=Asin(ωx+?)(A>0,ω>0,0<?<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则
(2013•海口二模)设偶函数f(x)=Asin(ωx+?)(A>0,ω>0,0<?<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则