题目内容
已知函数y=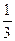 x3+x2+x的图像C上存在一定点P满足:若过点p的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),就恒有y1+y2为定值y0,则y0的值为( )
x3+x2+x的图像C上存在一定点P满足:若过点p的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),就恒有y1+y2为定值y0,则y0的值为( )
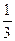 x3+x2+x的图像C上存在一定点P满足:若过点p的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),就恒有y1+y2为定值y0,则y0的值为( )
x3+x2+x的图像C上存在一定点P满足:若过点p的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),就恒有y1+y2为定值y0,则y0的值为( )A.-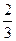 | B.-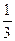 | C.-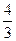 | D.-2 |
A
由y=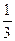 x3+x2+x=
x3+x2+x=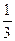 (x+1)3-
(x+1)3-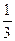 ,可得函数的对称中心为点(-1,-
,可得函数的对称中心为点(-1,-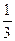 ),即得点P的坐标为(-1,-
),即得点P的坐标为(-1,-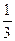 ),过点P的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),则M、N两点关于点P中心对称,所以y1+y2=2×(-
),过点P的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),则M、N两点关于点P中心对称,所以y1+y2=2×(-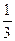 ),∴y0=-
),∴y0=-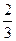 ,故应选A.
,故应选A.
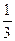 x3+x2+x=
x3+x2+x=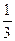 (x+1)3-
(x+1)3-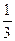 ,可得函数的对称中心为点(-1,-
,可得函数的对称中心为点(-1,-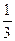 ),即得点P的坐标为(-1,-
),即得点P的坐标为(-1,-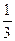 ),过点P的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),则M、N两点关于点P中心对称,所以y1+y2=2×(-
),过点P的直线l与曲线C交于不同于P的两点M(x1,y1),N(x2,y2),则M、N两点关于点P中心对称,所以y1+y2=2×(-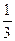 ),∴y0=-
),∴y0=-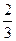 ,故应选A.
,故应选A.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
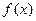 是定义在
是定义在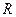 上的偶函数,对任意的
上的偶函数,对任意的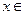 R都有
R都有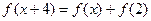 成立.若
成立.若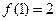 ,则
,则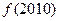 等于=
等于= 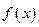 是定义在实数集上的奇函数,且
是定义在实数集上的奇函数,且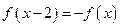 ,结出以下结论:
,结出以下结论: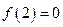 ;②
;②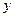 轴对称;④
轴对称;④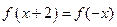
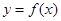 的值域是
的值域是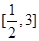 ,则函数
,则函数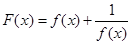 的值域是( )
的值域是( )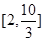
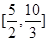
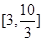

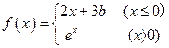 若
若 存在,则常数
存在,则常数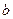 的值是( )
的值是( )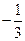
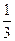
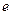
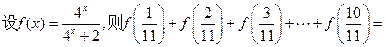 .
.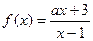 的反函数为
的反函数为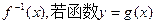 的图象与函数
的图象与函数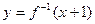 的图象关于直线
的图象关于直线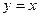 对称,且
对称,且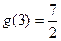 ,则实数a的值为( )
,则实数a的值为( )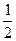
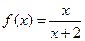 ,则
,则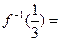 ☆☆☆☆☆☆ ;
☆☆☆☆☆☆ ;