Question

已知椭圆中心在原点，焦点在y轴上，焦距为4，离心率为．

（I）求椭圆方程；

（II）设椭圆在y轴的正半轴上的焦点为M，又点A和点B在椭圆上，且M分有向线段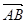所成的比为2，求线段AB所在直线的方程．

 

Answer 1

【答案】

（I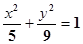）.     （II） ．

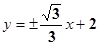【解析】本试题主要考查椭圆方程的求解，以及直线与椭圆的位置关系的综合运用，求解直线的方程的综合运用。

（1）利用椭圆的性质来表示得到参数ab,c的值，进而得到椭圆的方程。

（2）根据直线与椭圆方程联立方程组，然后得到二次方程，结合韦达定理得到根与系数的关系，由M分有向线段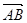所成的比为2，进而得到斜率的值