题目内容
(1)已知椭圆中心在原点,焦点在x轴,长轴长为短轴长的3倍,且过点P(3,2),求此椭圆的方程;
(2)求与双曲线
-
=1有公共渐近线,且焦距为8的双曲线的方程.
(2)求与双曲线
| x2 |
| 5 |
| y2 |
| 3 |
分析:(1)设椭圆的标准方程,代入点P(3,2),即可求椭圆的方程;
(2)设双曲线的方程为
-
=λ,利用曲线的焦距为8,建立方程,求出λ,即可得到双曲线的方程.
(2)设双曲线的方程为
| x2 |
| 5 |
| y2 |
| 3 |
解答:解:(1)设椭圆的标准方程为
+
=1(b>0)
∵椭圆过点P(3,2),∴
+
=1
∴b2=5
∴椭圆的方程为
+
=1; …(8分)
(2)设双曲线的方程为
-
=λ,即
-
=1
∵双曲线的焦距为8
∴5λ+3λ=±16
∴λ=±2
∴双曲线的方程为
-
=±1. …(16分)
| x2 |
| 9b2 |
| y2 |
| b2 |
∵椭圆过点P(3,2),∴
| 9 |
| 9b2 |
| 4 |
| b2 |
∴b2=5
∴椭圆的方程为
| x2 |
| 45 |
| y2 |
| 5 |
(2)设双曲线的方程为
| x2 |
| 5 |
| y2 |
| 3 |
| x2 |
| 5λ |
| y2 |
| 3λ |
∵双曲线的焦距为8
∴5λ+3λ=±16
∴λ=±2
∴双曲线的方程为
| x2 |
| 10 |
| y2 |
| 6 |
点评:本题考查椭圆与双曲线的标准方程,考查学生的计算能力,正确设出椭圆与双曲线的标准方程是关键.

练习册系列答案
相关题目
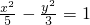 有公共渐近线,且焦距为8的双曲线的方程.
有公共渐近线,且焦距为8的双曲线的方程.