题目内容
 如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则①
如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则①| |PF| |
| |PD| |
| |QF| |
| |BF| |
| |AO| |
| |BO| |
| |AF| |
| |AB| |
| |FO| |
| |AO| |
| A、1个 | B、3个 | C、4个 | D、5个 |
分析:根据题意,设椭圆的方程为
+
=1,进而由椭圆的方程,分别化简表示、计算5个式子的值,与离心率e=
比较可得答案.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
解答:解:设椭圆的方程为
+
=1,(0<a<b)依次分析5个比值的式子可得:
①、根据椭圆的第二定义,可得
=e,故符合;
②、根据椭圆的性质,可得|BF|=
-c=
,|QF|=
,则
=
=e,故符合;
③、由椭圆的性质,可得|AO|=a,|BO|=
,则
=
=e,故符合;
④、由椭圆的性质,可得|AF|=a-c,|AB|=
-a=
(a-c),则
=
=e,故符合;
⑤、由椭圆的性质,可得|AO|=a,|FO|=c,
=
=e,故符合;
故选D.
| x2 |
| a2 |
| y2 |
| b2 |
①、根据椭圆的第二定义,可得
| |PF| |
| |PD| |
②、根据椭圆的性质,可得|BF|=
| a2 |
| c |
| b2 |
| c |
| b2 |
| a |
| |QF| |
| |BF| |
| c |
| a |
③、由椭圆的性质,可得|AO|=a,|BO|=
| a2 |
| c |
| |AO| |
| |BO| |
| c |
| a |
④、由椭圆的性质,可得|AF|=a-c,|AB|=
| a2 |
| c |
| a |
| c |
| |AF| |
| |AB| |
| c |
| a |
⑤、由椭圆的性质,可得|AO|=a,|FO|=c,
| |FO| |
| |AO| |
| c |
| a |
故选D.
点评:本题考查椭圆的性质,需要掌握椭圆的常见性质以及其中的一些特殊的长度,如|BF|=
-c=
,是焦准距.
| a2 |
| c |
| b2 |
| c |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
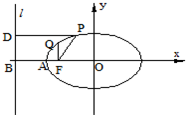 如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l(椭圆上的点到焦点的距离与到准线的距离之比等于离心率)交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则①
如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l(椭圆上的点到焦点的距离与到准线的距离之比等于离心率)交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则① 如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则椭圆的离心率是①
如图,已知椭圆中心在原点,F是焦点,A为顶点,准线l交x轴于点B,点P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则椭圆的离心率是①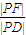 ;②
;②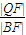 ;③
;③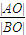 ;④
;④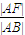 ;⑤
;⑤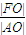 ,其中比值为椭圆的离心率的有( )
,其中比值为椭圆的离心率的有( )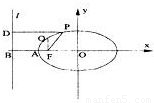
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,其中比值为椭圆的离心率的有( )
,其中比值为椭圆的离心率的有( )