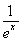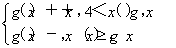题目内容
已知函数f(x)=1-2ax-a2x(a>1).
(1)求函数f(x)的值域;
(2)若x∈[-2,1]时,函数f(x)的最小值是-7,求a的值及函数f(x)的最大值.
(1)(-∞,1)(2)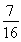
【解析】(1)由题意,知f(x)=2-(1+ax)2,因为ax>0,所以f(x)<2-1=1,所以函数f(x)的值域为(-∞,1).
(2)因为a>1,所以当x∈[-2,1]时,a-2≤ax≤a,于是fmin(x)=2-(a+1)2=-7,所以a=2,此时,函数f(x)的最大值为2-(2-2+1)2=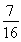 .
.

练习册系列答案
相关题目