题目内容
在等腰Rt△ABC中,∠A=90°,
=(1,2),
=(m,n),则
=( )
| AB |
| AC |
| BC |
| A、(0,-4)或(-2,0) |
| B、(0,4)或(2,0) |
| C、(0,-4) |
| D、(-2,0) |
分析:在等腰Rt△ABC中,∠A=90°,则
⊥
且|
|=|
|,联立方程组,解方程组可得答案.
| AB |
| AC |
| AB |
| AC |
解答:解:在等腰Rt△ABC中,∠A=90°,则
⊥
∴
•
=0,得m+2n=0,
又|
|=|
|,得m2+n2=5,
解得
或
,
∴
=(1,-2)或(-1,2),
=
-
=(0,-4)或(-2,0)
故选A.
| AB |
| AC |
∴
| AB |
| AC |
又|
| AB |
| AC |
解得
|
|
∴
| AC |
| BC |
| AC |
| AB |
故选A.
点评:若向量
=(x1,y1),
=(x2,y2),则
∥
?x1•x2+y1y2=0.即:“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0.
| a |
| b |
| a |
| b |

练习册系列答案
相关题目
在等腰Rt△ABC中,∠A=90°,
=(1,2),
=(m,n)(n>0)则
=( )
| AB |
| AC |
| BC |
| A、(-3,-1) |
| B、(-3,1) |
| C、(3,-1) |
| D、(3,1) |
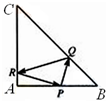 在等腰Rt△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到原来的点P.若AP=
在等腰Rt△ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到原来的点P.若AP=| 4 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在等腰Rt△ABC中,在斜边AB上任取一点M,求AM的长小于AC的长的概率.
在等腰Rt△ABC中,在斜边AB上任取一点M,求AM的长小于AC的长的概率.