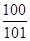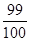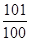题目内容
等差数列{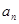 }的前n项和为
}的前n项和为 ,则常数
,则常数 = ( )
= ( )
| A.-2 | B.2 | C.0 | D.不确定 |
A
解析试题分析:因为 为等差数列的前n项和,所以
为等差数列的前n项和,所以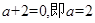 。
。
考点:等差数列的性质。
点评:熟记等差数列前n 项和的性质:等差数列前n项和的形式一定为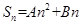 的形式,一定要注意不含常数项。这条性质在选择题和填空题中可以直接应用。
的形式,一定要注意不含常数项。这条性质在选择题和填空题中可以直接应用。

练习册系列答案
相关题目
等差数列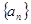 的前项
的前项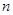 和为
和为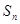 ,若
,若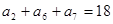 ,则
,则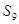 的值为( )
的值为( )
A.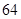 | B.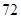 | C.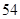 | D.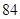 |
等差数列{an}的前n项和为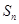 .已知
.已知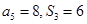 ,则
,则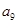 = ( )
= ( )
| A.8 | B.12 | C.16 | D.24 |
已知-1,a,b,-4成等差数列,-1,c,d, e,-4成等比数列,则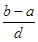 =( )
=( )
A.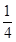 | B.-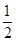 | C.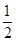 | D.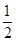 或- 或-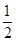 |
已知等差数列 中,
中,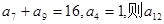 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
在等差数列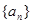 中,
中,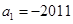 ,前n项和为
,前n项和为 ,且
,且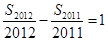 ,则
,则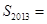
A.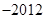 | B.2012 | C.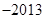 | D.2013 |
若△ABC的三个内角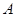 、
、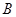 、
、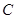 成等差数列,则
成等差数列,则
A.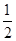 | B.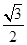 | C.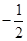 | D.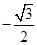 |
已知数列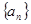 为等比数列,
为等比数列,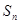 是它的前
是它的前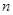 项和,若
项和,若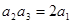 ,且
,且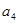 与
与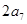 的等差中项为
的等差中项为 ,则
,则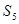 =
=
| A.35 | B.33 | C.31 | D.29 |
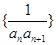 的前100项和为( )
的前100项和为( )