题目内容
已知数列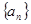 为等比数列,
为等比数列,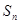 是它的前
是它的前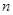 项和,若
项和,若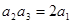 ,且
,且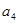 与
与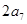 的等差中项为
的等差中项为 ,则
,则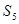 =
=
| A.35 | B.33 | C.31 | D.29 |
C
解析试题分析:因为根据已知条件设出首项和公比分别是a1和q,则结合等比数列的通项公式可知a2•a3=a1q•a1q2=2a1∴a4=2=2a4+2a7=a4+2a4q3=2× ∴求解得到q=
∴求解得到q=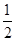 ,然后由于通项公式的性质可知a1=
,然后由于通项公式的性质可知a1=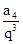 =16,故
=16,故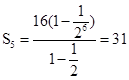 ,故选C。
,故选C。
考点:本题主要考查了等比数列的性质.属基础题
点评:对于数列问题,关键是运用基本元素a1和q表示出a2和a3代入a2•a3=2a1求得a4,再根据等差中项的性质得到a4+2a7=a4+2a4q3,求得q,进而求得a1,代入S5即可.

练习册系列答案
相关题目
等差数列{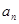 }的前n项和为
}的前n项和为 ,则常数
,则常数 = ( )
= ( )
| A.-2 | B.2 | C.0 | D.不确定 |
已知等差数列 的通项公式为
的通项公式为 ,则它的公差为( )
,则它的公差为( )
| A.2 | B.3 | C. | D. |
设等差数列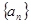 的前
的前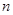 项和为
项和为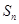 ,若
,若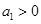 ,
,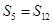 ,则当
,则当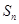 取得最大值时,
取得最大值时,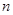 的值为
的值为
| A.7 | B.8 | C.9 | D.8或9 |
已知等差数列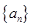 的通项公式
的通项公式 ,则
,则 等于 ( )
等于 ( )
| A.1 | B.2 | C.0 | D.9 |
已知数列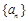 是公比为q的等比数列,且
是公比为q的等比数列,且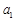 ,
,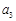 ,
,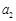 成等差数列,则q=
成等差数列,则q=
A.1或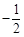 | B.1 | C.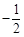 | D.-2 |
若实数a,b,c成等比数列,则函数 的图像与
的图像与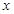 轴交点的个数为( )
轴交点的个数为( )
| A.0个 | B.1个 | C.2个 | D.不能确定 |
已知 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,
, ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
等差数列 中,
中, 则
则 ( )
( )
| A.31 | B.32 | C.33 | D.34 |