题目内容
(本题满分14分)设函数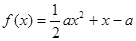 的定义域为
的定义域为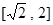 ,记函数
,记函数 的最大值为
的最大值为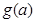 .
.
(1)求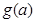 的解析式;(2)已知
的解析式;(2)已知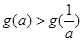 试求实数
试求实数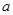 的取值范围.
的取值范围.
(1) 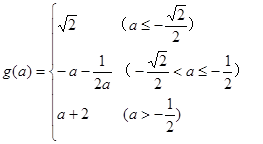 (2)
(2) 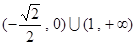
解析试题分析:(1) ( i )当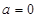 时,
时,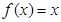 在
在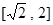 单调递增,
单调递增,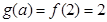 -----------1分
-----------1分
(ii)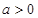 时,
时, 的对称轴为
的对称轴为 ,则
,则 在
在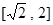 单调递增,
单调递增, 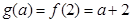 --------------2分
--------------2分
(iii)当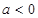 时,
时,  的对称轴为
的对称轴为 ,
,
若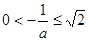 即
即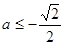 时
时 在
在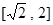 单调递减,
单调递减,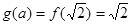 ------------------3分
------------------3分
若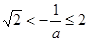 即
即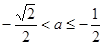 时
时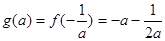 --------------------4分
--------------------4分
若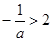 即
即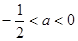 时
时 在
在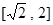 单调递增,
单调递增,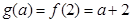 -----------------------5分
-----------------------5分
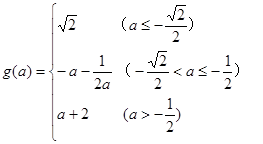 --------------------6分
--------------------6分
(2) 当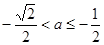 时
时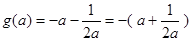 ,
,
设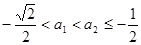 ,
,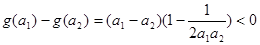 ------9分
------9分
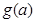 在区间
在区间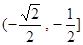 单调递增 -------------10分
单调递增 -------------10分
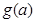 在
在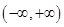 上不递减,
上不递减, 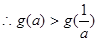 等价于
等价于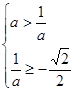 或
或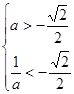 -----------12分
-----------12分
解得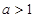 或
或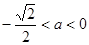 -------------------13分
-------------------13分
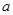 的取值范围是
的取值范围是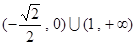 ----------14分
----------14分
考点:二次函数求最值及解不等式
点评:本题求最值时需分情况讨论,对学生来说是一个难点

练习册系列答案
相关题目
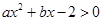 的解集是
的解集是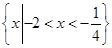 ,求
,求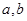 的值;
的值;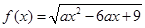 的定义域为
的定义域为 ,求实数
,求实数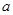 的取值范围.
的取值范围.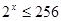 且
且 ,
,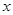 的取值范围;
的取值范围;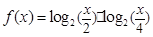 的最大值和最小值及对应的x值。
的最大值和最小值及对应的x值。 上的函数
上的函数 满足
满足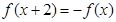 ,且当
,且当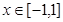 时,
时,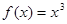 ,
, 上的表达式;
上的表达式;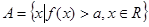 ,且
,且 ,求实数
,求实数 的取值范围。
的取值范围。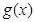 对任意实数
对任意实数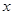 都满足
都满足 且
且
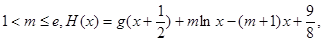 求证:
求证: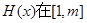 上为减函数;
上为减函数;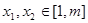 ,恒有
,恒有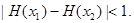
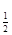 (log2 x)]=0,求x。;
(log2 x)]=0,求x。;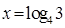 ,求
,求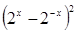 的值。
的值。 万美元,可获得加工费近似为
万美元,可获得加工费近似为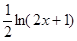 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失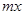 万美元,其中
万美元,其中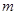 为该时段美元的贬值指数,
为该时段美元的贬值指数,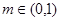 ,从而实际所得的加工费为
,从而实际所得的加工费为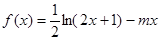 (万美元).
(万美元).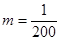 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随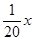 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为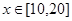 (其中
(其中