题目内容
设F1、F2是椭圆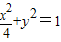
的两个焦点，点P在椭圆上，且△F1PF2的面积为1，则
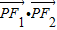的值为（ ）A．1
B．0
C．
D．2
【答案】分析：由题意，算出椭圆的焦点坐标，根据三角形面积公式算出P的纵坐标为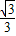
，从而得到第一象限内满足条件的点P坐标，从而得到向量
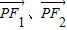的坐标，算出则
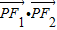的值．
解答：解：∵椭圆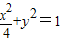
中，a=2，b=1
∴c=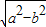
=
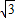，得椭圆的焦点为F1（-
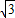，0），F2（
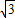，0）
设P的纵坐标为n，则△F1PF2的面积为S=
|F1F2|×n=1，
即
×
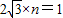，解之得n=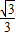
由椭圆的对称性，设P为第一象限的点，求得P的坐标为（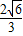
，
）
∴
，
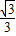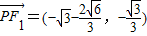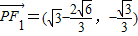
可得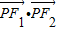
=（-
-
）（
-
）+（-
）（-
）=
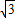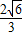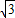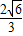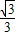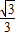-3+
=0
故选：B
点评：本题给出椭圆的焦点三角形的面积，求数量积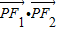
的值．着重考查了椭圆的定义与标准方程、向量的数量积等知识，属于中档题．
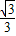，从而得到第一象限内满足条件的点P坐标，从而得到向量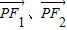的坐标，算出则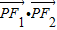的值．解答：解：∵椭圆
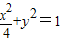中，a=2，b=1∴c=
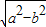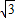=，得椭圆的焦点为F1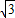（-，0），F2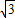（，0）设P的纵坐标为n，则△F1PF2的面积为S=
|F1F2|×n=1，即
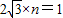×，解之得n=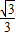由椭圆的对称性，设P为第一象限的点，求得P的坐标为（
，）∴
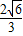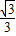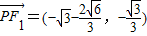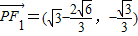
，可得
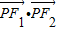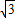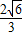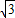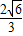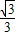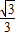=（--）（-）+（-）（-）=-3+=0故选：B
点评：本题给出椭圆的焦点三角形的面积，求数量积
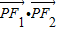的值．着重考查了椭圆的定义与标准方程、向量的数量积等知识，属于中档题． 
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
的两个焦点，P是椭圆上一点，且P到两个焦点的距离之差为2，则△PF1F2是（ ）
的两个焦点，点F1、F2到直线
的距离分别为d1、d2，试求d1·d2的值，并判断直线L与椭圆M的位置关系。
的两个焦点，点F1、F2到直线 
（m、n不同时为0）的距离分别为d1、d2，且直线L与椭圆M相切，试求d1·d2的值。
的两个焦点，以F1为圆心，且过椭圆中心的圆与椭圆的一个交点为M，若直线F2M与圆F1相切，则该椭圆的离心率是 
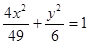的两个焦点，P是椭圆上的点，且
，
的面积为（ ）
D．