题目内容
8.已知数列{an}满足a1=2,an+1=$\frac{2}{1-{a}_{n}}$-1(n∈N+),则a2015的值为( )| A. | 2 | B. | -$\frac{1}{2}$ | C. | -3 | D. | $\frac{1}{3}$ |
分析 通过计算出前几项的值确定周期,进而计算可得结论.
解答 解:∵a1=2,an+1=$\frac{2}{1-{a}_{n}}$-1(n∈N+),
∴a2=$\frac{2}{1-{a}_{1}}$-1=$\frac{2}{1-2}-1$=-3,
a3=$\frac{2}{1-{a}_{2}}-1$=$\frac{2}{1+3}-1$=-$\frac{1}{2}$,
a4=$\frac{2}{1-{a}_{3}}-1$=$\frac{2}{1+\frac{1}{2}}-1$=$\frac{1}{3}$,
a5=$\frac{2}{1-{a}_{4}}-1$=$\frac{2}{1-\frac{1}{3}}-1$=2,
∴该数列是以4为周期的周期数列,
∵2015=503×4+3,
∴a2015=a3=-$\frac{1}{2}$,
故选:B.
点评 本题考查数列的通项,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.等差数列{an}的前n项和为Sn,已知a1=-12,S13=0,使得an>0的最小正整数n等于( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
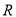 的函数
的函数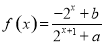 是奇函数.
是奇函数.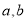 的值;
的值;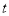 的不等式
的不等式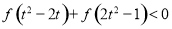 .
.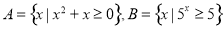 ,则
,则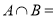 ( )
( )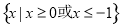 B.
B.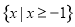
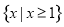 D.
D.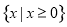

 如图:已知矩形BB1C1C所在平面与底面ABB1N垂直,直角梯形ABB1N中AN∥BB1,AB⊥AN,CB=BA=AN=2,BB1=4.
如图:已知矩形BB1C1C所在平面与底面ABB1N垂直,直角梯形ABB1N中AN∥BB1,AB⊥AN,CB=BA=AN=2,BB1=4. 中央电视台“星光大道”节目的现场观众来自4所学校,分别在图中的四个区域Ⅰ,Ⅱ,Ⅲ,Ⅳ坐定.有4种不同颜色的服装,同一学校的观众必须穿上同种颜色的服装,且相邻两个区域的颜色不同,不相邻区域颜色相同与否不受限制,那么不同着装方法有多少种?
中央电视台“星光大道”节目的现场观众来自4所学校,分别在图中的四个区域Ⅰ,Ⅱ,Ⅲ,Ⅳ坐定.有4种不同颜色的服装,同一学校的观众必须穿上同种颜色的服装,且相邻两个区域的颜色不同,不相邻区域颜色相同与否不受限制,那么不同着装方法有多少种?