题目内容
3.类比平面几何中的射影定理:若直角三角形ABC中(如图),AB、AC互相垂直,AD是BC边的高,则AB2=BD•BC;AC2=CD•BC.若在三棱锥A-BCD中(如图),三个侧面ABC、ACD、ADB两两互相垂直,O是点A在平面BCD上的投影,则三棱锥的侧面面积与它在底面上的投影面积和底面积的之间满足的关系为S△ABC2=S△DBC•S△BCO(只需填一个)
分析 首先猜想出结论,再进行证明:在△BCD内,延长DO交BC于E,连接AE,利用线面垂直的判定与性质可以证出AE⊥BC且DE⊥BC,从而AE、EO、ED分别是△ABC、△BCO、△BCD的边BC的高线,然后在Rt△ADE中,利用已知条件的结论得到AE2=EO•ED,再变形整理得到S△ABC2=S△DBC•S△BCO.
解答 解:结论:S△ABC2=S△DBC•S△BCD.
证明如下 在△BCD内,延长DO交BC于E,连接AE,
在△BCD内,延长DO交BC于E,连接AE,
∵AD⊥平面ABC,BC?平面ABC,
∴BC⊥AD,
同理可得:BC⊥AO
∵AD、AO是平面AOD内的相交直线,
∴BC⊥平面AOD
∵AE、DE?平面AOD
∴AE⊥BC且DE⊥BC
∵△AED中,EA⊥AD,AO⊥DE
∴根据题中的已知结论,得AE2=EO•ED
两边都乘以($\frac{1}{2}$BC)2,得($\frac{1}{2}$BC•AE)2=($\frac{1}{2}$BC•EO)•($\frac{1}{2}$BC•ED)
∵AE、EO、ED分别是△ABC、△BCO、△BCD的边BC的高线
∴S△ABC=$\frac{1}{2}$BC•AE,S△BC0=$\frac{1}{2}$BC•EO,S△BCD=$\frac{1}{2}$BC•ED
∴有S△ABC2=S△DBC•S△BC0.
故答案为:S△ABC2=S△DBC•S△BCO.
点评 本题以平面几何中的射影定理为例,将其推广到空间的一个正确的命题并加以证明,着重考查了类比推理和空间的线面垂直的判定与性质等知识点,属于基础题.

练习册系列答案
相关题目
8.已知数列{an}满足a1=2,an+1=$\frac{2}{1-{a}_{n}}$-1(n∈N+),则a2015的值为( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | -3 | D. | $\frac{1}{3}$ |
11.已知函数$f(x)=\frac{(sinx+cosx)-|sinx-cosx|}{2}$,则函数f(x)的值域为( )
| A. | [-1,1] | B. | [-1,$\frac{\sqrt{2}}{2}$] | C. | [-$\frac{\sqrt{2}}{2}$,1] | D. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] |
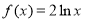 的图象与函数
的图象与函数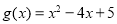 的图象的交点个数为( )
的图象的交点个数为( )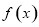 的图象过点
的图象过点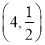 ,则
,则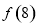 的值为( )
的值为( )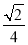 B.64 C.
B.64 C.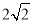 D.
D.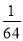
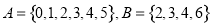 ,则
,则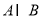 的真子集可以是( )
的真子集可以是( )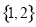 B.
B.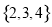 C.
C.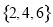 D.
D.