Question

（2008•扬州二模）设m为实数，A={(x，y)|

x-2y+5≥0 3-x≥0 mx+y≥0

}，B={（x，y）|x²+y²≤25}，若A⊆B，则m的取值范围是

[0，

4

3

]

．

Answer 1

分析：根据题意，作出集合A、B对应的平面区域，可得A对应图中三角形阴影区域而B表示圆x²+y²=25及其内部．讨论m的符号并将直线y=mx绕原点旋转，建立关于m的不等式，解之即可得到实数m的取值范围．

解答：解：由题意，作出A={(x，y)|

x-2y+5≥0 3-x≥0 mx+y≥0

}表示的平面区域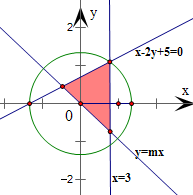
得到如图的阴影部分区域，
而集合B={（x，y）|x²+y²≤25}，表示圆x²+y²=25及其内部
∵A⊆B，∴集合A对应的区域全部落在B的圆及其内部
若-m＞0，则A中取到x＜-5的点，不能满足条件，故-m≤0，即m≥0．
当mx+y=0绕坐标原点旋转时，直线过B点时为边界位置，
此时-m=-

4

3

，可得m=

4

3

．再观察图形，
可得当0≤m≤

4

3

时，满足集合A对应的区域全部落在B的圆及其内部
∴m的取值范围是[0，

4

3

]．
故答案为：[0，

4

3

]

点评：本题给出不等式组表示的平面区域，在集合A的图形完全在集合B内部时求参数的范围．着重考查了圆的标准方程、直线的方程和不等式组表示的平面区域等知识，属于中档题．