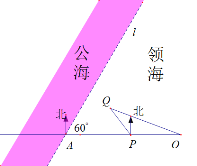
题目内容
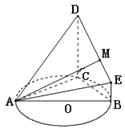
【题目】某海警基地码头![]() 的正西方向
的正西方向![]() 海里处有海礁界碑
海里处有海礁界碑![]() ,过点
,过点![]() 且与
且与![]() 成
成![]() 角(即北偏东
角(即北偏东![]() )的直线
)的直线![]() 为此处的一段领海与公海的分界线(如图所示)。在码头
为此处的一段领海与公海的分界线(如图所示)。在码头![]() 的正西方向且距离
的正西方向且距离![]() 点
点![]() 海里的领海海面
海里的领海海面![]() 处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从
处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从![]() 处即刻出发。若巡逻艇以可疑船的航速的
处即刻出发。若巡逻艇以可疑船的航速的![]() 倍
倍![]() 前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点
前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点![]() 处截获可疑船。
处截获可疑船。
(1)若可疑船的航速为![]() 海里
海里![]() 小时,
小时,![]() ,且可疑船沿北偏西
,且可疑船沿北偏西![]() 的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
(2)若要确保在领海内(包括分界线)成功拦截可疑船,求![]() 的最小值。
的最小值。
【答案】(1)![]() 小时;(2)
小时;(2)![]() 。
。
【解析】
(1) 设![]() ,则
,则![]() ,利用余弦定理求出a值,进而得到巡逻艇成功拦截可疑船所用的时间;
,利用余弦定理求出a值,进而得到巡逻艇成功拦截可疑船所用的时间;
(2)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的平面直角坐标系,则
轴的正方向,建立如图所示的平面直角坐标系,则![]() ,设
,设![]() ,可疑船被截获的轨迹是以
,可疑船被截获的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,利用直线与圆的位置关系得到结果.
为半径的圆,利用直线与圆的位置关系得到结果.
(1)因为巡逻艇的航速是可疑船的航速的2倍,可疑船的航速为![]() 海里/小时,所以巡逻艇的航速为
海里/小时,所以巡逻艇的航速为![]() 海里/小时,且
海里/小时,且![]() ,设
,设![]() ,则
,则![]() ,
,
又可疑船沿北偏西![]() 的方向朝公海逃跑,所以
的方向朝公海逃跑,所以![]() ,
,
在![]() 中,有
中,有![]() ,
,
即![]() ,故
,故![]() ,解得
,解得![]() (负值舍去)
(负值舍去)
所以![]() 小时。
小时。
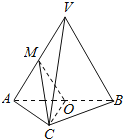
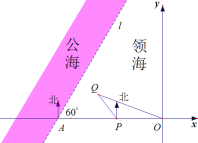
(2)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的平面直角坐标系,则
轴的正方向,建立如图所示的平面直角坐标系,则![]() ,设
,设![]() ,
,
因为巡逻艇的航速是可疑船的航速的![]() 倍,所以
倍,所以![]() ,
,
故![]() ,即
,即![]()
故可疑船被截获的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,
为半径的圆,
又直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
要确保在领海内(包括分界线)成功拦截可疑船,则:
圆心![]() 在直线
在直线![]() 下方,且
下方,且![]() 的轨迹与直线
的轨迹与直线![]() 至多只有一个公共点,
至多只有一个公共点,
所以![]() 且
且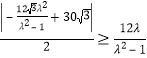
即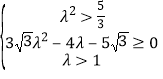 ,解得
,解得![]() ,
,
故要确保在领海内(包括分界线)成功拦截可疑船,则![]() 。
。

【题目】(1)从某厂生产的一批零件1000个中抽取20个进行研究,应采用什么抽样方法?
(2)对(1)中的20个零件的直径进行测量,得到下列不完整的频率分布表:(单位:mm)
分组 | 频数 | 频率 |
| 2 | |
| 6 | |
| 8 | |
| ||
合计 | 20 | 1 |
①完成频率分布表;
②画出其频率分布直方图.