题目内容
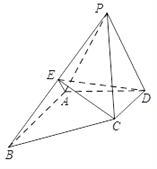
【题目】如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
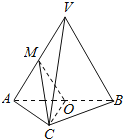
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V-ABC的体积.
【答案】(1)证明见解析;(2) 证明见解析;(3)![]()
【解析】
(1)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥平面MOC;
(2)证明OC⊥平面VAB,即可证明平面MOC⊥平面VAB
(3)利用等体积法求三棱锥V-ABC的体积
(1)证明:∵O,M分别为AB,VA的中点,
∴OM∥VB,
∵VB![]() 平面MOC,OM平面MOC,
平面MOC,OM平面MOC,
∴VB∥平面MOC;
(2)∵AC=BC,O为AB的中点,
∴OC⊥AB,
∵平面VAB⊥平面ABC,OC平面ABC,
∴OC⊥平面VAB,
∵OC平面MOC,
∴平面MOC⊥平面VAB
(3)在等腰直角三角形ACB中,AC=BC=![]() ,∴AB=2,OC=1,
,∴AB=2,OC=1,
∴等边三角形△VAB 中,S△VAB=![]() ,
,
∵OC⊥平面VAB,
∴VC-VAB=![]() S△VAB=
S△VAB=![]() ,
,
∴VV-ABC=VC-VAB=![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目