题目内容
设函数f(x)=x|x-a|+b,求证:f(x)为奇函数的充要条件是a2+b2=0.
【答案】
证明见试题解析.
【解析】
试题分析:充要条件的证明要分别证明充分性和必要性,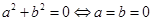 .本题充分性是由
.本题充分性是由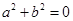 证明
证明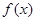 为奇函数,必要性是由
为奇函数,必要性是由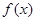 为奇函数证明
为奇函数证明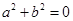 .
.
试题解析:证明充分性:∵a2+b2=0,∴a=b=0, 2
∴f(x)=x|x| 3
∵f(-x)=-x|-x|=-x|x|,-f(x)=-x|x|, 4
∴f(-x)=-f(x),∴f(x)为奇函数 6
必要性:若f(x)为奇函数,则对一切x∈R,f(-x)=-f(x)恒成立 7
即-x|-x-a|+b=-x|x-a|-b恒成立 8
令x=0,则b=-b,∴b=0, 10
令x=a,则2a|a|=0,∴a=0 11
即a2+b2=0 12
考点:充要条件

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
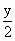 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.