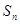题目内容
(本小题满分13分)
 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求A1B与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B-A1D-A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
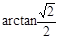 ,
,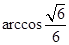 ,线段AC的中点F
,线段AC的中点F
【解析】解:(Ⅰ)连接A1C.∵A1B1C1-ABC为直三棱柱,∴CC1⊥底面ABC,∴CC1⊥BC.
∵AC⊥CB,∴BC⊥平面A1C1CA.
∴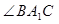 为
为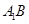 与平面A1C1CA所成角,
与平面A1C1CA所成角,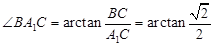 .
.
∴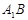 与平面A1C1CA所成角为
与平面A1C1CA所成角为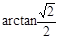 .
.
(Ⅱ)分别延长AC,A1D交于G. 过C作CM⊥A1G 于M,连结BM,
∵BC⊥平面ACC1A1,∴CM为BM在平面A1C1CA内的射影,
∴BM⊥A1G,∴∠CMB为二面角B—A1D—A的平面角,
平面A1C1CA中,C1C=CA=2,D为C1C的中点,
∴CG=2,DC=1 在直角三角形CDG中,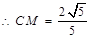 ,
,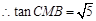 .
.
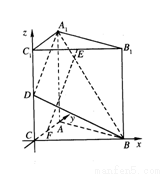 即二面角B—A1D—A的大小为
即二面角B—A1D—A的大小为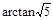 .
.
(Ⅲ)取线段AC的中点F,则EF⊥平面A1BD.
证明如下:
∵A1B1C1—ABC为直三棱柱,∴B1C1//BC,
∵由(Ⅰ)BC⊥平面A1C1CA,∴B1C1⊥平面A1C1CA,
∵EF在平面A1C1CA内的射影为C1F,当F为AC的中点时,
C1F⊥A1D,∴EF⊥A1D.
同理可证EF⊥BD,∴EF⊥平面A1BD.
解法二:
(Ⅰ)同解法一
(Ⅱ)∵A1B1C1—ABC为直三棱柱,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点.
建立如图所示的坐标系得:
C(0,0,0),B(2,0,0),A(0,2,0),
C1(0,0,2), B1(2,0,2), A1(0,2,2),
D(0,0,1), E(1,0,2).
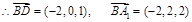 ,设平面A1BD的法向量为
,设平面A1BD的法向量为
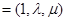 ,
,
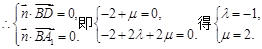
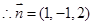 .
.
平面ACC1A1的法向量为 =(1,0,0),
=(1,0,0),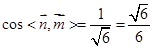 .
.
即二面角B—A1D—A的大小为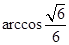 .
.
(Ⅲ)F为AC上的点,故可设其坐标为(0,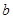 ,0),∴
,0),∴ .
.
由(Ⅱ)知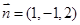 是平面A1BD的一个法向量,
是平面A1BD的一个法向量,
 欲使EF⊥平面A1BD,当且仅当
欲使EF⊥平面A1BD,当且仅当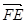 //
// .
.
∴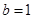 ,∴当F为AC的中点时,EF⊥平面A1BD.
,∴当F为AC的中点时,EF⊥平面A1BD.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程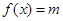 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数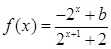 是奇函数.
是奇函数.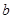 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性;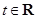 ,不等式恒成立
,不等式恒成立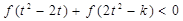 ,求k的取值范围.
,求k的取值范围.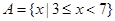 ,
,  ,
,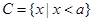 .
. (∁
(∁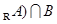 ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2,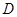 为
为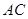 的中点。
的中点。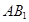 ∥平面
∥平面 ;
;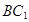 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn
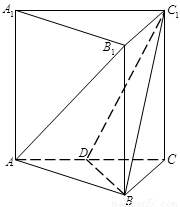
 为锐角,且
为锐角,且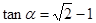 ,函数
,函数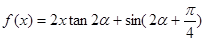 ,数列{
,数列{ }的首项
}的首项 .
.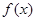 的表达式;
的表达式; 中,若
中,若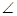 A=2
A=2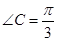 ,BC=2,求
,BC=2,求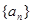 的前
的前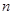 项和
项和