题目内容
18.设有双曲线$\frac{{x}^{2}}{2}$-y2=1,过点P(x0,1)的直线与双曲线交于点A,B,若点P不可能成为线段AB的中点,则x0的取值范围为[-2,-$\sqrt{2}$]∪[$\sqrt{2}$,2].分析 假设P为中点,设A(x1,y1),B(x2,y2),设过P的直线为x=my+x0-m,代入双曲线方程,运用判别式大于0,两根之和,求得x0的取值范围,取补集即可得到所求范围.
解答 解:假设P为中点,设A(x1,y1),B(x2,y2),
设过P的直线为x=my+x0-m,
代入双曲线方程,可得
(m2-2)y2+2m(x0-m)y+(x0-m)2-2=0,
则判别式△=4m2(x0-m)2-4(m2-2)[(x0-m)2-2]>0,
y1+y2=$\frac{2m(m-{x}_{0})}{{m}^{2}-2}$=2,
化简可得mx0=2,
即m=$\frac{2}{{x}_{0}}$,代入判别式,化简可得
x04-6x02+8>0,
解得x02>4或x02<2,
由点P不可能成为线段AB的中点,
则2≤x02≤4,
解得-2≤x0≤-$\sqrt{2}$或$\sqrt{2}$≤x0≤2.
故答案为:[-2,-$\sqrt{2}$]∪[$\sqrt{2}$,2].
点评 本题考查直线和双曲线的位置关系,考查中点坐标公式的运用,考查运算能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
 如图,EF是△ABC的中位线,AD是BC边上的中线,在以A,B,C,E,F为端点的有两条线段表示的向量中请分别写出:
如图,EF是△ABC的中位线,AD是BC边上的中线,在以A,B,C,E,F为端点的有两条线段表示的向量中请分别写出: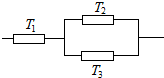 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}$,$\frac{3}{4}$,$\frac{3}{4}$,且是互相独立的.将它们中某两个元件并联后再和第三元件串联接入电路,在如图的电路中,电路不发生故障的概率是$\frac{15}{32}$.
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2}$,$\frac{3}{4}$,$\frac{3}{4}$,且是互相独立的.将它们中某两个元件并联后再和第三元件串联接入电路,在如图的电路中,电路不发生故障的概率是$\frac{15}{32}$.