题目内容
3.在△ABC中,AB=2AC=2,$\overrightarrow{AB}$•$\overrightarrow{AC}$=-1,若$\overrightarrow{AO}$=x1•$\overrightarrow{AB}$+x2•$\overrightarrow{AC}$(O是△ABC的外心),则x1+x2的值为$\frac{13}{6}$.分析 建立直角坐标系,求出三角形各顶点的坐标,因为O为△ABC的外心,把AB的中垂线 m方程和AC的中垂线 n的方程,联立方程组,求出O的坐标,利用已知向量间的关系,待定系数法求x1和x2 的值.
解答 解:如图:以A为原点,以AB所在的直线为x轴,建立直角系:则A(0,0),B (2,0),C(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).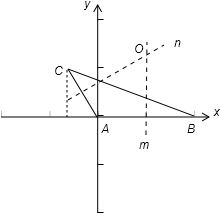
∵O为△ABC的外心,∴O在AB的中垂线m:x=1 上,又在AC的中垂线n 上.
∵AC的中点(-$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$),AC的斜率为-$\sqrt{3}$,
∴中垂线n的方程为y-$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{3}$(x+$\frac{1}{4}$).
把直线m和n 的方程联立方程组解得△ABC的外心O(1,$\frac{2\sqrt{3}}{3}$),
由条件若$\overrightarrow{AO}$=x1•$\overrightarrow{AB}$+x2•$\overrightarrow{AC}$得:(1,$\frac{2\sqrt{3}}{3}$)=x1(2,0)+x2(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)=(2x1-$\frac{1}{2}$x2,$\frac{\sqrt{3}}{2}$x2 ),
∴2x1-$\frac{1}{2}$x2=1,且$\frac{\sqrt{3}}{2}$x2=$\frac{2\sqrt{3}}{3}$,
∴x1=$\frac{5}{6}$,x2=$\frac{4}{3}$,
∴x1+x2=$\frac{13}{6}$,
故答案为:$\frac{13}{6}$.
点评 本题考查求两条直线的交点坐标的方法,三角形外心的性质,向量的坐标表示及向量相等的条件,待定系数法求参数值.属中档题.

| A. | 4 | B. | 2 | C. | 4i | D. | 2i |
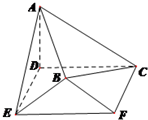 如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$.
如图,在空间几何体ABCDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=$\sqrt{2}$. 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.