题目内容
已知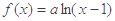 ,
,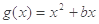 ,
,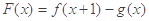 ,其中
,其中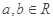 。
。
(1)若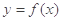 与
与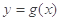 的图像在交点(2,
的图像在交点(2,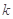 )处的切线互相垂直,
)处的切线互相垂直,
求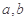 的值;
的值;
(2)若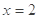 是函数
是函数 的一个极值点,
的一个极值点,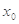 和1是
和1是 的两个零点,
的两个零点,
且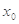 ∈(
∈(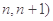
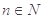 ,求
,求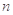 ;
;
(3)当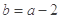 时,若
时,若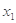 ,
,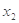 是
是 的两个极值点,当|
的两个极值点,当|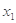 -
-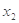 |>1时,
|>1时,
求证:|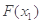 -
-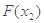 |
|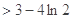
(1) (2)
(2)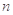 =3(3)
=3(3)
解析试题分析:(1)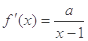 ,
, ,由
,由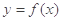 与
与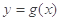 的图像在交点(2,
的图像在交点(2,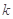 )处的切线互相垂直,可得
)处的切线互相垂直,可得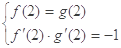 解之即可;
解之即可;
(2)由题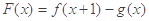 =
= ,
,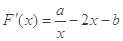
,由题知 可解得
可解得 ,故
,故 =6
=6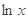 -(
-(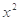 -
- ),
),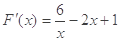 =
=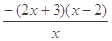 ,
,
讨论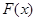 的单调性可得
的单调性可得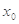 ∈(3,4),故
∈(3,4),故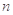 =3;
=3;
(3)当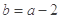 时,
时, =
=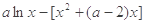 ,
,
讨论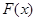 的单调性,|
的单调性,|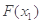 -
- |=
|= 极大值-
极大值- 极小值=F(-
极小值=F(-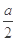 )―F(1)
)―F(1)
= ―
―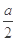 )+
)+
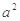 ―1,
―1,
设
讨论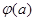 函数,求出其最小值,即得|
函数,求出其最小值,即得|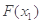 -
- |>3-4
|>3-4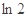
(1)解: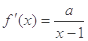 ,
,
由题知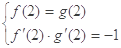 ,即
,即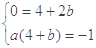 解得
解得
(2)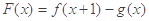 =
= ,
,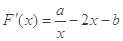
 =
=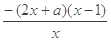 ,
,
由题知 ,即
,即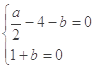 解得
解得 =6,
=6, =-1
=-1
∴ =6
=6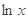 -(
-(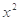 -
- ),
),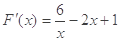 =
=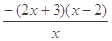
∵ >0,由
>0,由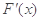 >0,解得0<
>0,解得0< <2;由
<2;由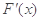 <0,解得
<0,解得 >2
>2
∴ 在(0,2)上单调递增,在(2,+∞)单调递减,
在(0,2)上单调递增,在(2,+∞)单调递减,
故 至多有两个零点,其中
至多有两个零点,其中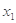 ∈(0,2),
∈(0,2),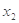 ∈(2, +∞)
∈(2, +∞)
又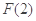 >
>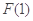 =0,
=0, =6(
=6(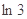 -1)>0,
-1)>0,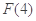

练习册系列答案
相关题目
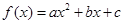 的图像过点
的图像过点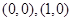 和
和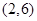 ,直线
,直线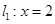 ,直线
,直线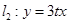 (其中
(其中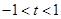 ,
,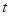 为常数);若直线
为常数);若直线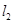 与函数
与函数 的图像以及直线
的图像以及直线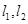 与函数
与函数 ;
;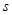 关于
关于 的解析式;
的解析式; 可作曲线
可作曲线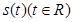 的三条切线,求实数
的三条切线,求实数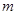 的取值范围.
的取值范围.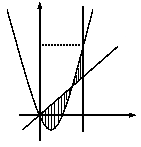
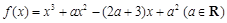 .
.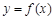 在
在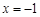 处的切线与直线
处的切线与直线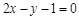 平行,求a的值;
平行,求a的值;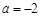 时,求
时,求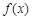 的单调区间.
的单调区间. .
.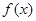 在
在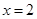 时取得极值,求实数
时取得极值,求实数 的值;
的值;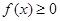 对任意
对任意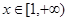 恒成立,求实数
恒成立,求实数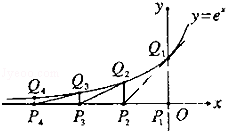
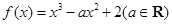 ,
,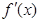 为
为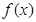 的导函数。 (1)求函数
的导函数。 (1)求函数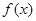 的单调递减区间;
的单调递减区间;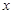 ,有
,有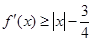 成立,求
成立,求 的取值范围;
的取值范围; 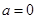 时,在曲线
时,在曲线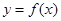 上是否存在两点
上是否存在两点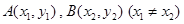 ,使得曲线在
,使得曲线在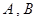 两点处的切线均与直线
两点处的切线均与直线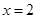 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由. .
. ,求曲线
,求曲线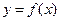 在点
在点 处的切线方程;
处的切线方程; 求函数
求函数 的单调区间;
的单调区间; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。 在区间
在区间 上为单调增函数,求
上为单调增函数,求 的取值范围.
的取值范围.