题目内容
已知椭圆C: 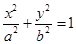 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.
(I)求椭圆C的方程;
(II)若斜率为k的直线过点M(2,0),且与椭圆C相交于A, B两点.试探讨k为何值时,三角形OAB为直角三角形.
(I) 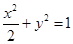 (II)
(II)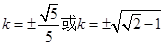
解析试题分析:(I)由已知可得b=c=1,再由a2=b2+c2,解出a即可.(II)设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-2),代入椭圆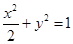 中,得到关于x的一元二次方程,由判别式求出k的取值范围,和用k表示的x1+x2,x1x2的表达式,然后分以O或A或B为直角顶点,根据向量垂直的坐标表示的充要条件列出关于k的方程,求解即可.
中,得到关于x的一元二次方程,由判别式求出k的取值范围,和用k表示的x1+x2,x1x2的表达式,然后分以O或A或B为直角顶点,根据向量垂直的坐标表示的充要条件列出关于k的方程,求解即可.
试题解析:(Ⅰ)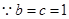
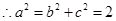
所以椭圆方程为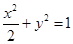
(Ⅱ)由已知直线AB的斜率存在,设AB的方程为: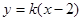
由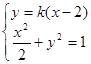 得
得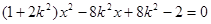
,得: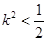 ,即
,即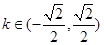
设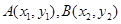 ,
, 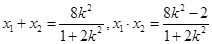
(1)若 为直角顶点,则
为直角顶点,则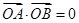 ,即
,即 ,
, 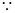
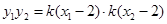 ,所以上式可整理得,
,所以上式可整理得, 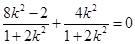 ,解,得
,解,得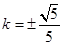 ,满足
,满足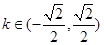
(2)若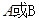 为直角顶点,不妨设以
为直角顶点,不妨设以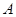 为直角顶点,
为直角顶点,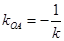 ,则
,则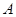 满足:
满足: 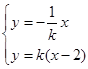 ,解得
,解得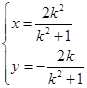 ,代入椭圆方程,整理得,
,代入椭圆方程,整理得,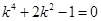

解得,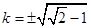 ,满足
,满足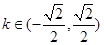

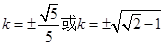 时,三角形
时,三角形 为直角三角形
为直角三角形
考点:1.椭圆方程及其性质;2.直线与椭圆的相交的条件;3.向量垂直的充要条件.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 是椭圆
是椭圆 :
: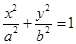
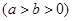 上一点,
上一点, 分别为
分别为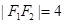 ,
,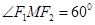 ,
,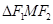 的面积为
的面积为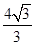 .
.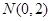 ,过点
,过点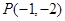 作直线
作直线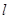 ,交椭圆
,交椭圆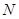 的
的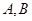 两点,直线
两点,直线 的斜率分别为
的斜率分别为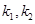 ,证明:
,证明: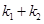 为定值.
为定值.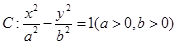 经过点
经过点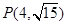 ,且双曲线
,且双曲线 的渐近线与圆
的渐近线与圆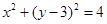 相切.
相切.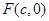 是双曲线
是双曲线 是双曲线
是双曲线 为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.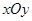 中,已知曲线
中,已知曲线 上任意一点到点
上任意一点到点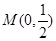 的距离与到直线
的距离与到直线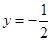 的距离相等.
的距离相等.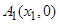 ,
,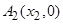 是
是 轴上的两点
轴上的两点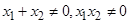 ,过点
,过点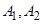 分别作
分别作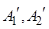 ,直线
,直线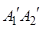 与x轴交于点
与x轴交于点 ,这样就称
,这样就称 确定了
确定了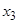 .同样,可由
.同样,可由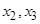 确定了
确定了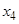 .现已知
.现已知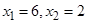 ,求
,求 :
: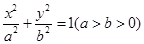 的离心率为
的离心率为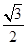 ,以椭圆
,以椭圆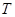 为圆心作圆
为圆心作圆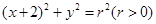 ,设圆
,设圆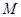 与点
与点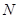 .
.
 的最小值,并求此时圆
的最小值,并求此时圆 是椭圆
是椭圆 分别与
分别与 轴交于点
轴交于点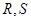 ,
,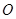 为坐标原点,
为坐标原点,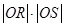 为定值.
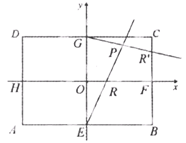
为定值.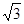 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且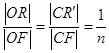 .
.
 :
: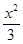 +
+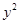 =1上;
=1上;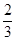 ,求证:直线MN过定点.
,求证:直线MN过定点.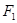 、
、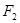 分别是椭圆
分别是椭圆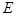 :
: 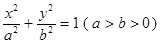 的左、右焦点,点
的左、右焦点,点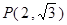 在直线
在直线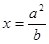 上,线段
上,线段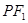 的垂直平分线经过点
的垂直平分线经过点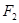 .直线
.直线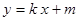 与椭圆
与椭圆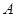 、
、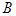 ,且椭圆
,且椭圆 ,使
,使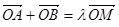 ,其中
,其中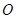 是坐标原点,
是坐标原点,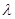 是实数.
是实数.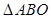 的面积最大?最大面积等于多少?
的面积最大?最大面积等于多少?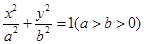 的右焦点为
的右焦点为 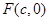 ,
, 为椭圆的上顶点,
为椭圆的上顶点,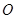 为坐标原点,且两焦点和短轴的两端构成边长为
为坐标原点,且两焦点和短轴的两端构成边长为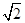 的正方形.
的正方形.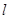 交与椭圆于
交与椭圆于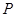 ,
, 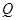 ,且使
,且使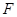 为
为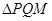 的垂心,若存在,求出
的垂心,若存在,求出