题目内容
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 的最小值为1,此时直线
的最小值为1,此时直线![]() :
:![]()
【解析】
(1)用直接法求轨迹方程,即设动点为![]() ,把已知用坐标表示并整理即得.注意取值范围;
,把已知用坐标表示并整理即得.注意取值范围;
(2)设![]() :
:![]() ,将其与曲线
,将其与曲线![]() 的方程联立,消元并整理得
的方程联立,消元并整理得![]() ,
,
设![]() ,
,![]() ,则可得
,则可得![]() ,
,![]() ,由
,由![]() 求出
求出![]() ,
,
将直线![]() 方程
方程![]() 与
与![]() 联立,得
联立,得![]() ,求得
,求得![]() ,计算
,计算![]() ,设
,设![]() .显然
.显然![]() ,构造
,构造![]() ,由导数的知识求得其最小值,同时可得直线
,由导数的知识求得其最小值,同时可得直线![]() 的方程.
的方程.
(1)设![]() ,则
,则![]() ,即
,即![]()
整理得![]()
(2)设![]() :
:![]() ,将其与曲线
,将其与曲线![]() 的方程联立,得
的方程联立,得![]()
即![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
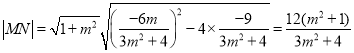
将直线![]() :
:![]() 与
与![]() 联立,得
联立,得![]()
∴![]()
∴
设![]() .显然
.显然![]()
构造![]()
![]() 在
在![]() 上恒成立
上恒成立
所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取“=”
时取“=”
即![]() 的最小值为1,此时直线
的最小值为1,此时直线![]() :
:![]() .
.
(注:1.如果按函数![]() 的性质求最值可以不扣分;2.若直线方程按斜率是否存在讨论,则可以根据步骤相应给分.)
的性质求最值可以不扣分;2.若直线方程按斜率是否存在讨论,则可以根据步骤相应给分.)

练习册系列答案
相关题目