题目内容
给定集合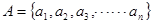
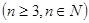 ,定义
,定义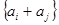
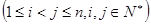 中所有不同
中所有不同
值的个数为集合A中的元素和的容量,用L(A)表示。若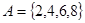 ,则L(A)= ;若数列
,则L(A)= ;若数列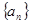 是等差数列,设集合
是等差数列,设集合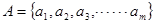
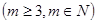 ,则L(A)关于m的表达式为
,则L(A)关于m的表达式为
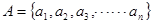
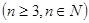 ,定义
,定义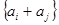
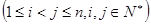 中所有不同
中所有不同值的个数为集合A中的元素和的容量,用L(A)表示。若
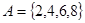 ,则L(A)= ;若数列
,则L(A)= ;若数列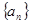 是等差数列,设集合
是等差数列,设集合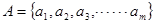
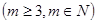 ,则L(A)关于m的表达式为
,则L(A)关于m的表达式为 5 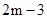
解:∵A={2,4,6,8},
∴ai+aj(1≤i<j≤4,i,j∈N)分别为:2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,
其中2+8=10,4+6=10,
∴定义ai+aj(1≤i<j≤4,i,j∈N)中所有不同值的个数为5,
即当A={2,4,6,8}时,L(A)=5.
当数列{an}是等差数列,且集合A={a1,a2,a 3,…,a m}(其中m∈N*,m为常数)时,
ai+aj(1≤i<j≤m,i,j∈N)的值列成如下各列所示图表:
a1+a2,a2+a3,a3+a4,…,am-2+am-1,am-1+am,
a1+a2,a2+a4,a3+a5,…,am-2+am,
…,…,…,…,
a1+am-2,a2+am-1,a3+am,
a1+am-1,a2+am,a1+am,
∵数列{an}是等差数列,
∴a1+a4=a2+a3,
a1+a5=a2+a4,
…,
a1+am=a2+am-1,
∴第二列中只有a2+am的值和第一列不重复,即第二列剩余一个不重复的值,
同理,以后每列剩余一个与前面不重复的值,
∵第一列共有m-1个不同的值,后面共有m-1列,
∴所有不同的值有:m-1+m-2=2m-3,
即当集合A={a1,a2,a 3,…,a m}(其中m∈N*,m为常数)时,L(A)=2m-3.
∴ai+aj(1≤i<j≤4,i,j∈N)分别为:2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,
其中2+8=10,4+6=10,
∴定义ai+aj(1≤i<j≤4,i,j∈N)中所有不同值的个数为5,
即当A={2,4,6,8}时,L(A)=5.
当数列{an}是等差数列,且集合A={a1,a2,a 3,…,a m}(其中m∈N*,m为常数)时,
ai+aj(1≤i<j≤m,i,j∈N)的值列成如下各列所示图表:
a1+a2,a2+a3,a3+a4,…,am-2+am-1,am-1+am,
a1+a2,a2+a4,a3+a5,…,am-2+am,
…,…,…,…,
a1+am-2,a2+am-1,a3+am,
a1+am-1,a2+am,a1+am,
∵数列{an}是等差数列,
∴a1+a4=a2+a3,
a1+a5=a2+a4,
…,
a1+am=a2+am-1,
∴第二列中只有a2+am的值和第一列不重复,即第二列剩余一个不重复的值,
同理,以后每列剩余一个与前面不重复的值,
∵第一列共有m-1个不同的值,后面共有m-1列,
∴所有不同的值有:m-1+m-2=2m-3,
即当集合A={a1,a2,a 3,…,a m}(其中m∈N*,m为常数)时,L(A)=2m-3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
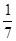 是较少两份面包数之和,问最少的1份面包数为
是较少两份面包数之和,问最少的1份面包数为 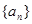 的各项均为正数,
的各项均为正数,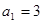 ,前
,前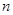 项和为
项和为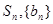 为等比数列,公比
为等比数列,公比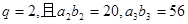 ; (1)求
; (1)求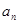 与
与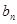 ; (2)求数列
; (2)求数列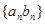 的前
的前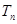 ; (3)记
; (3)记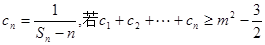 对任意正整数
对任意正整数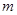 的取值范围。
的取值范围。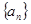 是等差数列,且
是等差数列,且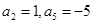
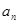 。②求
。②求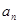 }的前n项和记为Sn.已知
}的前n项和记为Sn.已知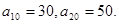
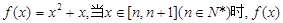 的所有整数值的个数为g(n) .
的所有整数值的个数为g(n) .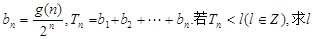 的最小值
的最小值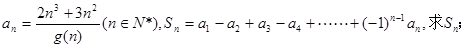
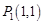 ,
,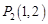 ,
,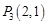 ,
,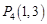 ,
,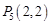 ,
,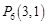 ,
,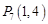 ,
,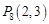 ,
,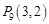 ,
,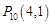 ,
,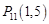 ,
,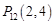 ,……,则
,……,则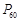 的坐标为( )
的坐标为( )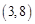
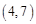
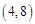
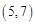
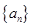 的前
的前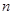 项和为
项和为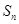 ,若
,若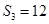 ,且
,且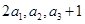 成等比数列.
成等比数列.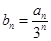 ,记数列
,记数列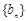 的前
的前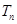 ,求
,求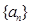 满足
满足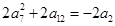 ,数列
,数列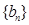 是等比数列,且
是等比数列,且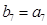 ,则
,则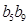 =( )
=( )