题目内容
(2012•道里区三模)选修4-5:不等式选讲
设不等式|2x-1|<1的解集为M,且a∈M,b∈M.
(Ⅰ) 试比较ab+1与a+b的大小;
(Ⅱ) 设maxA表示数集A中的最大数,且h=max{
,
,
},求h的范围.
设不等式|2x-1|<1的解集为M,且a∈M,b∈M.
(Ⅰ) 试比较ab+1与a+b的大小;
(Ⅱ) 设maxA表示数集A中的最大数,且h=max{
| 2 | ||
|
| a+b | ||
|
| 2 | ||
|
分析:(1)先解不等式得出其解集M,再利用作差法比较大小即可;
(2)不妨设0<a≤b<1,先找出其最大值,进而即可求出其范围.
(2)不妨设0<a≤b<1,先找出其最大值,进而即可求出其范围.
解答:解:由不等式|2x-1|<1化为-1<2x-1<1解得0<x<1,
∴原不等式的解集M={x|0<x<1},
(Ⅰ)∵a,b∈M,∴0<a<1,0<b<1.
∴(ab+1)-(a+b)=(1-a)(1-b)>0,
∴ab+1>a+b.
(Ⅱ)∵a,b∈M,∴0<a<1,0<b<1.
不妨设0<a≤b<1,则
≥
,∴
≥
;
=
+
<
+
≤
.
故
最大,即h=
>2.
∴h∈(2,+∞).
∴原不等式的解集M={x|0<x<1},
(Ⅰ)∵a,b∈M,∴0<a<1,0<b<1.
∴(ab+1)-(a+b)=(1-a)(1-b)>0,
∴ab+1>a+b.
(Ⅱ)∵a,b∈M,∴0<a<1,0<b<1.
不妨设0<a≤b<1,则
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
| 2 | ||
|
| a+b | ||
|
| ||
|
| ||
|
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
故
| 2 | ||
|
| 2 | ||
|
∴h∈(2,+∞).
点评:熟练掌握绝对值不等式的解法、作差法比较数的大小及不等式的基本性质是解题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
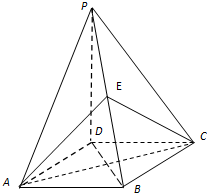 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=