题目内容
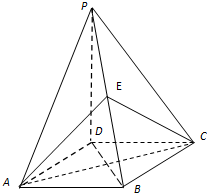 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(Ⅰ)求证:平面AEC⊥平面PDB;
(Ⅱ)当PD=
| 2 |
| PE |
| EB |
分析:(Ⅰ)设AC交BD于O,连接OE,由PD⊥平面ABCD,知PD⊥AC,由BD⊥AC,知AC⊥平面PBD,由此能够证明平面ACE⊥平面PBD.
(Ⅱ)法一:由平面ACE⊥平面PBD,知AO⊥PBD,由直线AE与平面PBD成角为45°,知∠AEO=45°,由此能够求出
.
法二:以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,利用向量法能够求出
的值.
(Ⅱ)法一:由平面ACE⊥平面PBD,知AO⊥PBD,由直线AE与平面PBD成角为45°,知∠AEO=45°,由此能够求出
| PE |
| EB |
法二:以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,利用向量法能够求出
| PE |
| EB |
解答:解:(Ⅰ)设AC交BD于O,连接OE,
∵PD⊥平面ABCD,∴PD⊥AC,
∵BD⊥AC,∴AC⊥平面PBD,
又∵AC⊆平面AEC,∴平面ACE⊥平面PBD.…(6分)
(Ⅱ)(方法一)∵平面ACE⊥平面PBD,平面ACE∩平面PBD=BD
AO⊥BD
∴AO⊥面PBD,
∵直线AE与平面PBD成角为45°,∴∠AEO=45°,
设PD=
AB=2,则OE=1,
∴
=1.…(12分)
(方法二)以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,如图
平面BDE法向量为
=(1,-1,0),
设PD=
AB=2,E(
λ,
λ,2-2λ),
=(
,
,-2),
令
=λ
,
则
=(
λ-
,
λ,2-2λ),
=
,
得λ=
或λ=1(舍),
∴
=1.…(12分)
∵PD⊥平面ABCD,∴PD⊥AC,
∵BD⊥AC,∴AC⊥平面PBD,
又∵AC⊆平面AEC,∴平面ACE⊥平面PBD.…(6分)
(Ⅱ)(方法一)∵平面ACE⊥平面PBD,平面ACE∩平面PBD=BD
AO⊥BD
∴AO⊥面PBD,

∵直线AE与平面PBD成角为45°,∴∠AEO=45°,
设PD=
| 2 |
∴
| PE |
| EB |
(方法二)以DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系,如图
平面BDE法向量为
| n |
设PD=
| 2 |
| 2 |
| 2 |
| PB |
| 2 |
| 2 |
令
| PE |
| PB |
则
| AE |
| 2 |
| 2 |
| 2 |
|
| ||||
|
|
| ||
| 2 |
得λ=
| 1 |
| 2 |
∴
| PE |
| BE |
点评:本题考查平面与平面垂直的证明,考查点的位置的确定.解题时要认真审题,仔细解答,注意空间思维能力的培养.

练习册系列答案
相关题目
 (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=