题目内容
(2012•道里区三模)已知函数f(x)=
,则下列关于函数y=f[f(x)]+1的零点个数的判断正确的是( )
|
分析:因为函数f(x)为分段函数,函数y=f(f(x))+1为复合函数,故需要分类讨论,确定函数y=f(f(x))+1的解析式,从而可得函数y=f(f(x))+1的零点个数;
解答:解:解:分四种情况讨论.
(1)x>1时,lnx>0,∴y=f(f(x))+1=ln(lnx)+1,此时的零点为x=e
>1;
(2)0<x<1时,lnx<0,∴y=f(f(x))+1=klnx+1,则k>0时,有一个零点,k<0时,klnx+1>0没有零点;
(3)若x<0,kx+1≤0时,y=f(f(x))+1=k2x+k+1,则k>0时,kx≤-1,k2x≤-k,可得k2x+k≤0,y有一个零点,
若k<0时,则k2x+k≥0,y没有零点,
(4)若x<0,kx+1>0时,y=f(f(x))+1=ln(kx+1)+1,则k>0时,即y=0可得kx+1=
,y有一个零点,k<0时kx>0,y没有零点,
综上可知,当k>0时,有4个零点;当k<0时,有1个零点;
故选B;
(1)x>1时,lnx>0,∴y=f(f(x))+1=ln(lnx)+1,此时的零点为x=e
| 1 |
| e |
(2)0<x<1时,lnx<0,∴y=f(f(x))+1=klnx+1,则k>0时,有一个零点,k<0时,klnx+1>0没有零点;
(3)若x<0,kx+1≤0时,y=f(f(x))+1=k2x+k+1,则k>0时,kx≤-1,k2x≤-k,可得k2x+k≤0,y有一个零点,
若k<0时,则k2x+k≥0,y没有零点,
(4)若x<0,kx+1>0时,y=f(f(x))+1=ln(kx+1)+1,则k>0时,即y=0可得kx+1=
| 1 |
| e |
综上可知,当k>0时,有4个零点;当k<0时,有1个零点;
故选B;
点评:本题考查分段函数,考查复合函数的零点,解题的关键是分类讨论确定函数y=f(f(x))+1的解析式,考查学生的分析能力,是一道中档题;

练习册系列答案
相关题目
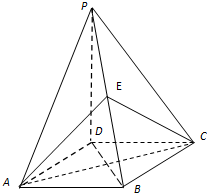 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=