题目内容
15.已知抛物线的顶点在原点,其准线过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点,又若抛物线与双曲线相交于点A($\frac{3}{2}$,$\sqrt{6}$),B($\frac{3}{2}$,-$\sqrt{6}$),求此两曲线的方程.分析 由抛物线与双曲线相交于点A($\frac{3}{2}$,$\sqrt{6}$),B($\frac{3}{2}$,-$\sqrt{6}$),先求出抛物线方程为y2=4x,从而得到a2+b2=1,由此能求出双曲线的方程.
解答 解:由题意可设抛物线方程为y2=2px,p>0,
将$x=\frac{3}{2}$,y=$\sqrt{6}$代入得p=2,所求抛物线的方程为y2=4x,…(4分)
其准线方程为x=-1,即双曲线的半焦距c=1,∴a2+b2=1,①,
又$\frac{(\frac{3}{2})^{2}}{{a}^{2}}-\frac{6}{{b}^{2}}=1$,②,
由①②可得${a}^{2}=\frac{1}{4}$,b2=$\frac{3}{4}$,
所求双曲线的方程为4x2-$\frac{4}{3}{y}^{2}$=1.…(8分)
点评 本题考查抛物线方程和双曲线方程的求法,是基础题,解题时要认真审题,注意双曲线和抛物线的性质的合理运用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.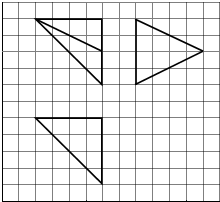 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )| A. | 8 | B. | $4\sqrt{5}$ | C. | 12 | D. | 16 |
3.在等比数列{an}中,a1=3,a6=6,则a16等于( )
| A. | 6 | B. | 12 | C. | 24 | D. | 48 |
10.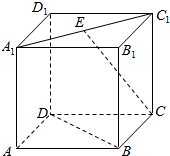 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
 如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )
如图,在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
5.已知定义域为R的偶函数f(x)在(0,+∞)上为增函数,则( )
| A. | f(4)>f(3) | B. | f(-5)>f(5) | C. | f(-3)>f(-5) | D. | f(3)>f(-6) |