题目内容
12.已知圆x2+y2=1,从这个圆上任意一点P向y轴作垂线段,求线段中点M的轨迹方程.分析 写出点P所在圆的方程,设出M、P的坐标,由中点坐标公式把P的坐标用M的坐标表示,把P的坐标代入圆的方程后整理得线段PP′中点M的轨迹方程.
解答 解:点P向y轴作垂线段,设为PP′.
由题意可得已知圆的方程为x2+y2=1.
设点M的坐标为(x,y),点P的坐标为(x0,y0),
∵M是线段PP′的中点,
∴由中点坐标公式得2x=x0,y=y0,
∵P(x0,y0)在圆x2+y2=1上,
∴(2x)2+y2=1①
即线段中点M的轨迹方程为4x2+y2=1.
点评 本题考查了轨迹方程的求法,训练了利用代入法求曲线方程,是中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20.设a=(lg3)2,b=30.3,c=lg$\sqrt{3}$,则( )
| A. | a<c<b | B. | c<a<b | C. | b<a<c | D. | b<c<a |
17.如果质点A按规律s=3t2运动,则在t=2时的瞬时速度是( )
| A. | 4 | B. | 6 | C. | 12 | D. | 24 |
4.已知集合$A=\{x|x>0\},B=\{x|\frac{1}{2}<{2^x}<4\}$,则A∩∁RB=( )
| A. | {x|x>0} | B. | {x|0<x<2} | C. | {x|x≥2} | D. | {x|x>2} |
2.已知sinθ=$\frac{m-3}{m+5}$,cosθ=$\frac{4-2m}{m+5}$($\frac{π}{2}$<θ<π),则tanθ=( )
| A. | $-\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
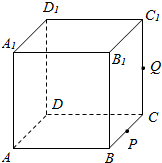 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.