题目内容

设A(x1，y1)，B(x2，y2)是椭圆＝1(a>b>0)上的两点，已知向量

若m·n＝0且椭圆的离心率e＝，短轴长为2，O为坐标原点．

(1)求椭圆的方程；

(2)若直线AB的斜率存在且直线AB过椭圆的焦点F(0，c)(c为半焦距)，求直线AB的斜率k的值；

(3)试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由．

.

(2)由题意，设直线AB的方程为y＝kx＋，

即y＝4x.

又A(x1，y1)在椭圆上，

所以S△AOB＝|x1|·|y1－y2|＝|x1|·|y1|＝1，

所以△AOB的面积为定值．

②当直线AB的斜率存在时，设直线AB的方程为y＝kx＋b.

所以△AOB的面积为定值．

练习册系列答案
相关题目
设A(x1，y1)，B(4，
9
5
)，C(x2，y2)是右焦点为F的椭圆
x2
25
+
y2
9
=1上三个不同的点，则“|AF|，|BF|，|CF|成等差数列”是“x1+x2=8”的（　　）
A、充要条件
B、必要不充分条件
C、充分不必要条件
D、既非充分也非必要
设
a
=(x1，y1)，
b
=(x2，y2)，若|
a
|=2，|
b
|=3，
a
•
b
=-6，则
x1+y1
x2+y2
=（　　）
A、
2
3
B、
3
2
C、-
2
3
D、-
3
2
设
a
=(x1，y1)，
b
=(x2，y2)，定义一种运算：
a
⊕
b
=（x1x2，y1y2）．已知
p
=(
8
π
，2)，
m
=(
1
2
，1)，
n
=(
π
4
，-
1
2
)．
（1）证明：（
p
⊕
m
）⊥
n
；
（2）点P（x0，y0）在函数g（x）=sinx的图象上运动，点Q（x，y）在函数y=f（x）的图象上运动，且满足
OQ
=
m
⊕
OP
+
n
（其中O为坐标原点），求函数f（x）的单调递减区间．

（09年莱阳一中学段检测）(14分)

      已知函数， (a>0且a1)，其中为常数．如果

h(x)=f(x)+g(x)是增函数，且h(x)的导函数h (x)存在零点．

    (1)求a的值；

    (2)设A(x1、y1)、B(x2、y2)(x1 < x2)是函数y=g(x)的图象上两点， 

(g(x)为g(x)的导函数)，证明：x1 < x0 < x2

．（本题满分12分）

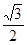设A(x1，y1)，B(x2，y2)，是椭圆+=(a＞b＞0)上的两点，已知向量m=(，)，n=(，)，若m·n=0且椭圆的离心率e=，短轴长为2，O为坐标原点.

(Ⅰ)求椭圆的方程;

(Ⅱ)试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网