题目内容
设
=(x1,y1),
=(x2,y2),定义一种运算:
⊕
=(x1x2,y1y2).已知
=(
,2),
=(
,1),
=(
,-
).
(1)证明:(
⊕
)⊥
;
(2)点P(x0,y0)在函数g(x)=sinx的图象上运动,点Q(x,y)在函数y=f(x)的图象上运动,且满足
=
⊕
+
(其中O为坐标原点),求函数f(x)的单调递减区间.
| a |
| b |
| a |
| b |
| p |
| 8 |
| π |
| m |
| 1 |
| 2 |
| n |
| π |
| 4 |
| 1 |
| 2 |
(1)证明:(
| p |
| m |
| n |
(2)点P(x0,y0)在函数g(x)=sinx的图象上运动,点Q(x,y)在函数y=f(x)的图象上运动,且满足
| OQ |
| m |
| OP |
| n |
分析:(1)根据该运算的定义,先求出
⊕
,然后只需证明(
⊕
)•
=0即可;
(2)由
=
⊕
+
可得x和x0的方程组,消掉x0可得f(x),利用余弦函数的单调性可求得答案;
| p |
| m |
| p |
| m |
| n |
(2)由
| OQ |
| m |
| OP |
| n |
解答:解:(1)
=(
,2),
=(
,1),依题意得
⊕
=(
,2),
又
=(
,-
),∴(
⊕
)•
=
×
+2×(-
)=0,
∴(
⊕
)⊥
;
(2)
=(x0,sinx0),
=(x,y),由足
=
⊕
+
,得
(x,y)=(
x0+
,sinx0-
),即
,
消去x0,得y=sin(2x-
)-
=-cos2x-
,即f(x)=-cos2x-
,
令2kπ-π≤2x≤2kπ(k∈Z),得kπ-
≤x≤kπ(k∈Z),
∴函数的单调递减区间是[kπ-
,kπ](k∈Z).
| p |
| 8 |
| π |
| m |
| 1 |
| 2 |
| p |
| m |
| 4 |
| π |
又
| n |
| π |
| 4 |
| 1 |
| 2 |
| p |
| m |
| n |
| 4 |
| π |
| π |
| 4 |
| 1 |
| 2 |
∴(
| p |
| m |
| n |
(2)
| OP |
| OQ |
| OQ |
| m |
| OP |
| n |
(x,y)=(
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
|
消去x0,得y=sin(2x-
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令2kπ-π≤2x≤2kπ(k∈Z),得kπ-
| π |
| 2 |
∴函数的单调递减区间是[kπ-
| π |
| 2 |
点评:本题考查三角恒等变换、复合函数的单调性,考查学生对问题的理解应用能力.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
设A(x1,y1),B(4,
),C(x2,y2)是右焦点为F的椭圆
+
=1上三个不同的点,则“|AF|,|BF|,|CF|成等差数列”是“x1+x2=8”的( )
| 9 |
| 5 |
| x2 |
| 25 |
| y2 |
| 9 |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既非充分也非必要 |
设
=(x1,y1),
=(x2,y2),若|
|=2,|
|=3,
•
=-6,则
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 +
+ =(a>b>0)上的两点,已知向量m=(
=(a>b>0)上的两点,已知向量m=( ,
, ),n=(
),n=( ,
, ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=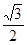 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.