题目内容
在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是____________.
等腰三角形
解:由正弦定理和内角和定理,可得
2cosBsinA=sinC=sin(A+B),所以得到cosBsinA=cosAsinB,sin(B-A)=0
所以B=A,说明了三角形为等腰三角形。
2cosBsinA=sinC=sin(A+B),所以得到cosBsinA=cosAsinB,sin(B-A)=0
所以B=A,说明了三角形为等腰三角形。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
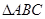 中,
中,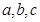 ,分别是角
,分别是角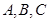 所对边的长,
所对边的长, ,且
,且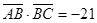
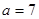 ,求角C.
,求角C.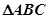 中,内角
中,内角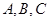 所对的边分别为
所对的边分别为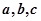 ,且
,且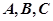 成等差数列.
成等差数列.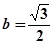 ,求
,求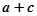 的取值范围;
的取值范围;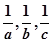 也成等差数列,求
也成等差数列,求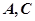 的大小.
的大小.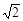 (sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为
(sin2A-sin2C)=(a-b)sinB,△ABC外接圆半径为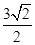 a
a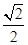 a
a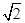 a
a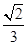 a
a
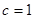 ,则最短边的长等于( )
,则最短边的长等于( )



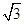 ,B=60°,则sinC=__________
,B=60°,则sinC=__________  中,内角
中,内角 的对边分别是
的对边分别是 ,且
,且 ,
, ,
,  ,求边长
,求边长 和
和
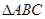 中,角
中,角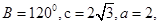 则此三角形的面积是 ;
则此三角形的面积是 ;