题目内容
在数列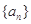 中,
中,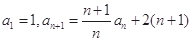 ,设
,设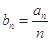
(1)证明数列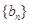 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)求所有正整数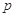 的值,使得
的值,使得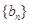 中某个连续
中某个连续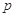 项的和是数列
项的和是数列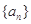 中的第8项.
中的第8项.
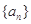 中,
中,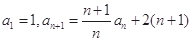 ,设
,设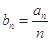
(1)证明数列
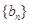 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;(2)求所有正整数
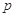 的值,使得
的值,使得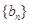 中某个连续
中某个连续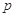 项的和是数列
项的和是数列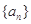 中的第8项.
中的第8项.(1)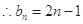 (2)
(2)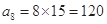
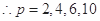
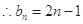 (2)
(2)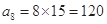
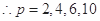
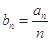 ,思路是在原来的递推公式
,思路是在原来的递推公式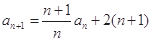 中变形出
中变形出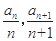 ,
,数列
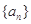 中的第8项是
中的第8项是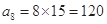 ,
,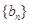 中某个连续
中某个连续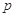 项的和表达出来是
项的和表达出来是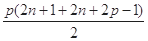
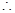
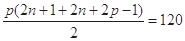 。
。证明(1)由已知得
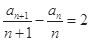 ……… 2分
……… 2分 即
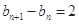 ,又
,又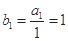
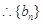 是以1为首项,2为公差的等差数列, ……… 4分
是以1为首项,2为公差的等差数列, ……… 4分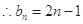 ………5分
………5分(2)易得
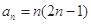 ,
,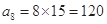 …7分
…7分令
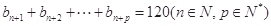 ……8分
……8分即
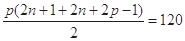
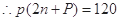 ……10分
……10分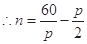 ,
,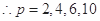

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
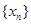 满足:
满足: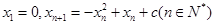
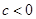
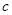 的取值范围,使数列
的取值范围,使数列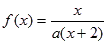 ,方程
,方程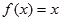 有唯一解,已知
有唯一解,已知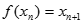
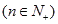 ,且
,且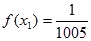 .
.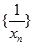 为等差数列,并求数列
为等差数列,并求数列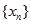 的通项公式;
的通项公式;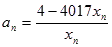 ,且
,且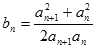
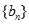 的前
的前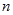 项和
项和 .
.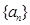 的前n项和为
的前n项和为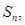 若
若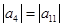 ,且公差
,且公差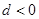 ,则当
,则当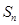 取最大值时,
取最大值时, 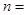 __________.
__________.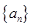 中,
中,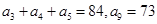 .
.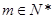 ,将数列
,将数列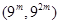 内的项的个数记为
内的项的个数记为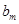 ,求数列
,求数列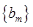 的前
的前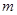 项和
项和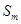 .
.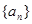 、
、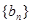 的前
的前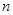 项和分别为
项和分别为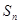 和
和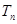 ,若
,若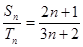 ,则
,则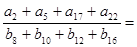 ( )
( )
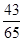
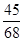
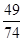
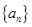 中,
中,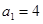 ,
,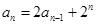 (
(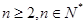 ).
).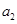 和
和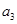 的值;
的值;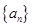 的通项公式.
的通项公式.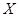 的分布列如右图:其中
的分布列如右图:其中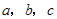 成等差数列,若
成等差数列,若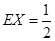 ,则
,则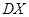 的值是 .
的值是 .
 的等差数列
的等差数列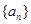 的前
的前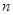 项和为
项和为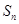 ,且
,且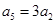 ,则下列数列不是等比数列的是( )
,则下列数列不是等比数列的是( )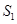 、
、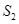 、
、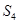 .
.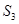 、
、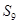 .
. 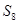 .
.