题目内容
(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为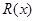 万元,且
万元,且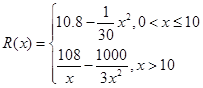 .
.
(I)写出年利润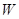 (万元)关于年产量
(万元)关于年产量 (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
(1)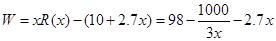
(2)当年产量为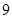 千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为
千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为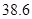 万元.
万元.
解析试题分析:解:(I)当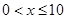 时,
时,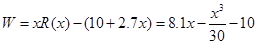 ;
;
当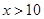 时,
时,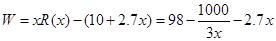 .
.
∴ 年利润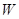 (万元)关于年产量
(万元)关于年产量 (千件)的函数关系式为
(千件)的函数关系式为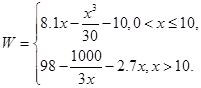
(Ⅱ)当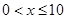 时,由
时,由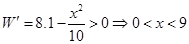 ,
,
即年利润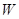 在
在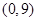 上单增,在
上单增,在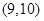 上单减
上单减
∴ 当 时,
时,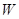 取得最大值,且
取得最大值,且 (万元).
(万元).
当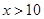 时,
时,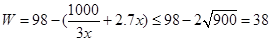 ,仅当
,仅当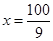 时取“=”
时取“=”
综上可知,当年产量为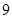 千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为
千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为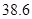 万元.
万元.
考点:本试题考查了函数模型在实际生活中的的运用。
点评:解决应用题,首先是审清题意,然后利用已知的关系式表述出利润函数:收入-成本=利润。将实际问题转换为代数式,然后利用函数的性质,或者均值不等式来求解最值,但是要注明定义域,属于中档题。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 的图象关于
的图象关于 轴对称,且在区间
轴对称,且在区间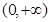 上是减函数,
上是减函数, 的解析式;((2)若
的解析式;((2)若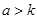 ,比较
,比较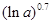 与
与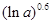 的大小;
的大小;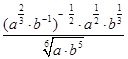 ;
;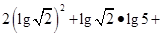
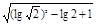 .
.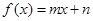 与指数型函数
与指数型函数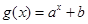 ,(
,(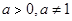 )的图像交于两点
)的图像交于两点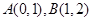 ,解答下列各题
,解答下列各题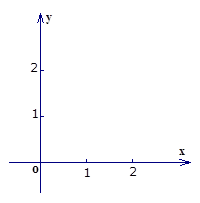 :
: 和指数型函数
和指数型函数 的表达式;
的表达式; 时,
时,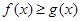 ;当
;当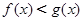 。
。 为常数,且
为常数,且 )满足条件:
)满足条件: ,且方程
,且方程 有两个相等的实数根.
有两个相等的实数根. 的解析式;
的解析式; 上的最大值和最小值;
上的最大值和最小值;
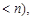 使
使 和
和 ,如果存在,求出
,如果存在,求出 的值,如不存在,请说明理由.
的值,如不存在,请说明理由. 的图象关于原点对称。
的图象关于原点对称。 在
在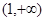 上的单调性,并根据定义证明。
上的单调性,并根据定义证明。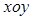 ,
, 轴在地平面上,
轴在地平面上,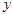 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在 表示的曲线上,其中
表示的曲线上,其中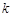 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标.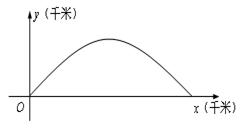
 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.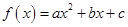 ,且
,且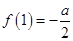 ,
,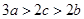 ,求证:(1)
,求证:(1)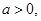 且
且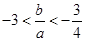 ;
; 在区间
在区间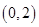 内至少有一个零点;
内至少有一个零点; 是函数
是函数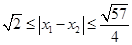 .
.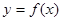 的图象过点(0,—3),且
的图象过点(0,—3),且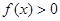 的解集(1,3)。
的解集(1,3)。 的解析式;
的解析式;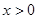 时,恒有
时,恒有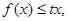 求实数t的取值范围。
求实数t的取值范围。