题目内容
(本题满分13分)设函数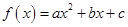 ,且
,且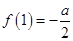 ,
,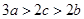 ,求证:(1)
,求证:(1)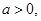 且
且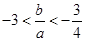 ;
;
(2)函数 在区间
在区间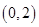 内至少有一个零点;
内至少有一个零点;
(3)设 是函数
是函数 的两个零点,则
的两个零点,则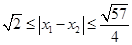 .
.
(1)根据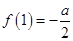 ,求出
,求出 ,再根据
,再根据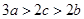 即可得证;(2)先求出
即可得证;(2)先求出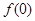 和
和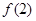 ,根据零点存在定理分
,根据零点存在定理分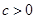 和
和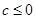 讨论即可得证;
讨论即可得证;
(3)利用韦达定理和第(1)问的结论即可得证.
解析试题分析:(1)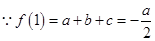 ,
,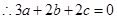 ,
,
又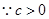 ,
,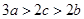 ,
,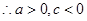 , ……2分
, ……2分
又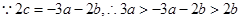
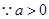
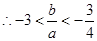 . ……4分
. ……4分
(2)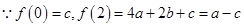
①当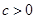 时,
时,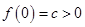 ,
,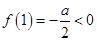
 函数
函数 在区间
在区间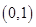 内至少有一个零点
内至少有一个零点
②当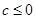 时,
时,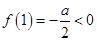 ,
,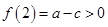 ,
,
函数 在区间
在区间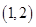 内至少有一个零点
内至少有一个零点
综上所述:函数 在区间
在区间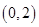 内至少有一个零点。 ……8分
内至少有一个零点。 ……8分
(3)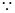
 是函数
是函数 的两个零点,
的两个零点,
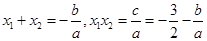

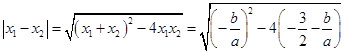
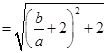
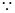
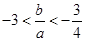 ,
,
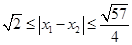 . ……13分
. ……13分
考点:本小题主要考查不等式的性质、函数的零点存在定理和韦达定理的应用,考查学生的推理论证能力.
点评:证明此类问题时,要充分利用不等式的性质和题设条件,尽量每一步都做到言之有据.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为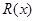 万元,且
万元,且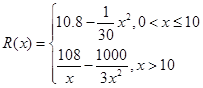 .
.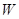 (万元)关于年产量
(万元)关于年产量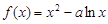 在
在 是增函数,
是增函数,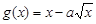 在(0,1)为减函数.
在(0,1)为减函数.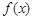 、
、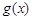 的表达式;
的表达式;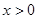 时,方程
时,方程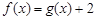 有唯一解;
有唯一解;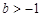 时,若
时,若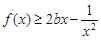 在
在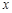 ∈
∈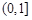 内恒成立,求
内恒成立,求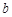 的取值范围.
的取值范围. (0<
(0<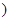 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,则当
,则当
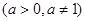 的定义域为集合
的定义域为集合 ,集合
,集合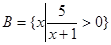 .
.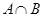 ,并说明理由。
,并说明理由。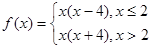 .
.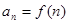 ,写出数列
,写出数列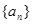 的前5项;
的前5项;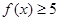 .
.