题目内容
已知函数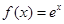 ,
,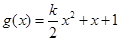 .
.
(1)当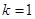 时,证明:
时,证明: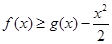 ;
;
(2)若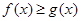 ,求k的取值范围.
,求k的取值范围.
(1)证明过程详见解析;(2)(-∞,0].
解析试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值、不等式的基本性质等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力,考查学生的函数思想.第一问,先将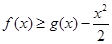 转化为
转化为 ,先得到
,先得到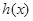 表达式,对
表达式,对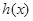 求导,利用“
求导,利用“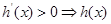 单调递增;
单调递增;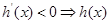 单调递减”解不等式求函数
单调递减”解不等式求函数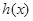 的单调区间,利用函数的单调性确定最小值所在的位置;第二问,将
的单调区间,利用函数的单调性确定最小值所在的位置;第二问,将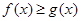 转化为
转化为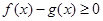 ,令F(x)=f(x)-g(x)对f(x)求导,由于
,令F(x)=f(x)-g(x)对f(x)求导,由于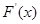 的正负不明显,所以进行二次求导,二次求导后得到G¢(x)=ex-k,只需讨论k的正负,通过
的正负不明显,所以进行二次求导,二次求导后得到G¢(x)=ex-k,只需讨论k的正负,通过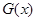 的单调性,求出
的单调性,求出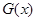 的最值,来判断
的最值,来判断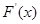 的正负,来判断
的正负,来判断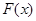 的单调性,从而求
的单调性,从而求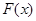 的最值.
的最值.
(1)当k=1时,设h(x)=f(x)-g(x)+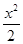 =ex-x-1,h¢(x)=ex-1. 1分
=ex-x-1,h¢(x)=ex-1. 1分
当x∈(-∞,0)时,h¢(x)<0,h(x)单调递减;
当x∈(0,+∞)时,h¢(x)>0,h(x)单调递增.
所以h(x)≥h(0)=0.
故f(x)≥g(x)-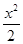 . 4分
. 4分
(2)设F(x)=f(x)-g(x)=ex-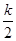 x2-x-1,则F¢(x)=ex-kx-1.
x2-x-1,则F¢(x)=ex-kx-1.
设G(x)=ex-kx-1,则G¢(x)=ex-k. 6分
(1)若k≤0时,则G¢(x)>0,G(x)单调递增,
当x∈(-∞,0)时,G(x)<G(0)=0,即F¢(x)<0,F(x)单调递减;
当x∈(0,+∞)时,G(x)>G(0)=0,即F¢(x)>0,F(x)单调递增.
故F(x)≥F(0)=0,此时f(x)≥g(x). 9分
(2)若k>0,则
当x∈(-∞,-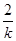 )时,ex-1<0,-
)时,ex-1<0,-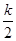 x2-x=-
x2-x=-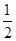 x(kx+2)<0,
x(kx+2)<0,
从而F(x)=ex-1-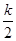 x2-x<0,这时f(x)≥g(x)不成立. 11分
x2-x<0,这时f(x)≥g(x)不成立. 11分
综上,k的取值范围是(-∞,0]. 12分
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的最值、不等式的基本性质.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案 .
. 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和 .
. 在
在 处的切线与直线
处的切线与直线 平行,求a的值;
平行,求a的值; 时,求
时,求 的单调区间.
的单调区间.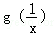 的大小关系;
的大小关系; 对任意x>0成立.
对任意x>0成立. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; .若至少存在一个
.若至少存在一个 ,使得
,使得 成立,求实数
成立,求实数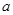 的取值范围.
的取值范围.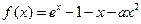 。
。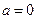 ,求
,求 的单调区间;
的单调区间;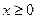 时,
时,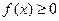 ,求a的取值范围。
,求a的取值范围。 .
. 在点
在点 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值; 时,求
时,求 ,
,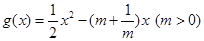 ,且
,且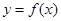 在点
在点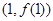 处的切线方程为
处的切线方程为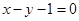 .
.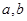 的值;
的值;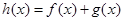 在区间
在区间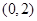 内有且仅有一个极值点,求
内有且仅有一个极值点,求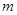 的取值范围;
的取值范围; 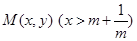 为两曲线
为两曲线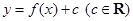 ,
,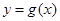 的交点,且两曲线在交点
的交点,且两曲线在交点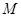 处的切线分别为
处的切线分别为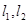 .若取
.若取 ,试判断当直线
,试判断当直线 轴围成等腰三角形时
轴围成等腰三角形时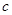 值的个数并说明理由.
值的个数并说明理由.