题目内容
【题目】已知圆C1:![]() 与y轴交于O,A两点,圆C2过O,A两点,且直线C2O恰与圆C1相切;
与y轴交于O,A两点,圆C2过O,A两点,且直线C2O恰与圆C1相切;
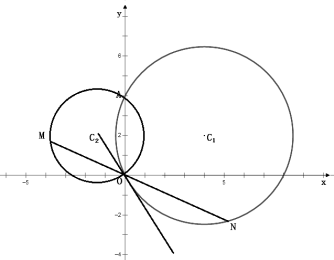
(1)求圆C2的方程。
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在,求出定点坐标,若不存在,说明理由。
【答案】(1)![]() ;(2)存在,且为
;(2)存在,且为![]() .
.
【解析】
试题分析:(1)由圆![]() 方程求得它与
方程求得它与![]() 轴交点
轴交点![]() 坐标,可设圆
坐标,可设圆![]() 的一般方程
的一般方程![]() ,利用O,A在圆
,利用O,A在圆![]() 上可得
上可得![]() ,这样可写出圆心
,这样可写出圆心![]() 坐标,利用切线即
坐标,利用切线即![]() 可求得
可求得![]() ;(2)如果存在,则
;(2)如果存在,则![]() 在线段
在线段![]() 的中垂线上,假设直线
的中垂线上,假设直线![]() 方程为
方程为![]() ,与两圆方程联立可解得
,与两圆方程联立可解得![]() 坐标,求出线段
坐标,求出线段![]() 的垂直平分线的方程,由直线方程观察它是否过一个定点,如果过定点就是所要求的
的垂直平分线的方程,由直线方程观察它是否过一个定点,如果过定点就是所要求的![]() 点.
点.
试题解析:(1)O(0,0),A(0,4),设圆C2的方程为![]() ,易得F=0,E=-4.故C2(-
,易得F=0,E=-4.故C2(-![]() ),由C2O⊥C1O得D=2,故圆C2的方程为
),由C2O⊥C1O得D=2,故圆C2的方程为![]() 。
。
(2)存在,设MN直线方程为y=kx,分别与圆C1、圆C2联立
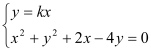 与
与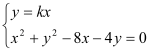 求得M(
求得M(![]() ,
,![]() ),
),
N(![]() ,
,![]() ),中点H(
),中点H(![]() ,
,![]() ),中垂线方程为:
),中垂线方程为:
![]() ,化简为:
,化简为:![]()
恒过定点(3,4)即为所求点P。

练习册系列答案
相关题目