题目内容
点A为△BCD所在平面外的一点,点O为点A在平面BCD内的射影,若AC⊥BD,AD⊥BC,求证:AB⊥CD.
分析:由已知中点A为△BCD所在平面外的一点,点O为点A在平面BCD内的射影,可得AO⊥BC,AO⊥BD,AO⊥CD,进而利用线面垂直与线线垂直之间的辩证关系,我们易得到O为△BCD的垂心,再由线面垂直的判定定理得到CD⊥平面AOB,最后由线面垂直的性质得到AB⊥CD.
解答:证明:由已知中点O为点A在平面BCD内的射影,
∴AO⊥平面BCD,即AO⊥BC,AO⊥BD,AO⊥CD
∵AC⊥BD,AC∩AO=A
∴BD⊥平面OAC,BD⊥CO,
同理由AD⊥BC可证BC⊥D0,
即O为△BCD的垂心,
∴CD⊥OB,又由OB∩AO=0
∴CD⊥平面AOB
又由AB?平面AOB
∴AB⊥CD
∴AO⊥平面BCD,即AO⊥BC,AO⊥BD,AO⊥CD
∵AC⊥BD,AC∩AO=A
∴BD⊥平面OAC,BD⊥CO,
同理由AD⊥BC可证BC⊥D0,
即O为△BCD的垂心,
∴CD⊥OB,又由OB∩AO=0
∴CD⊥平面AOB
又由AB?平面AOB
∴AB⊥CD
点评:本题考查的知识点是直线与平面垂直的性质,其中熟练掌握空间直线与平面垂直的判定定理及性质定理,是解答本题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
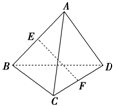 如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
