题目内容

17．在长为16cm的线段AB上任取一点C，现做一矩形，邻边长分别为AC，BC的长，则该矩形的面积大于60cm2的概率为$\frac{1}{4}$．

分析 设AC=x，则BC=16-x，由矩形的面积S=x（16-x）＞60可求x的范围，利用几何概率的求解公式可求．

解答 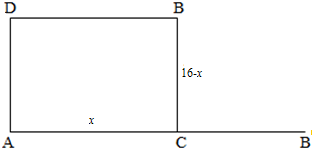解：设AC=x，则BC=16-x（0＜x＜16）
矩形的面积S=x（16-x）＞60，
∴x2-16x+60＜0
∴6＜x＜10
由几何概率的求解公式可得，矩形面积大于60cm2的概率P=$\frac{10-6}{16}=\frac{4}{16}$=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．

点评 本题主要考查了二次不等式的解法，与区间长度有关的几何概率的求解公式的应用，属于基础试题．

练习册系列答案
相关题目
7．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，且经过点（0，1）．圆C1：x2+y2=a2+b2．
（1）求椭圆C的方程；
（2）若直线l：y=kx+m（k≠0）与椭圆C有且只有一个公共点M，且l与圆C1相交于A，B两点，问$\overrightarrow{AM}+\overrightarrow{BM}$=0是否成立？请说明理由．
8．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）经过点（1，$\frac{3}{2}}$），且椭圆的左、右焦点分别为F1（-1，0）、F2（1，0），过椭圆的右焦点F2作两条互相垂直的直线，分别交椭圆于点 A、B及C、D．
（1）求椭圆的方程；
（2）求$\frac{1}{{|{{A}{B}}|}}$+$\frac{1}{{|{CD}|}}$的值；
（3）求|AB|+$\frac{9}{16}$|CD|的最小值．
5．已知a＞0，命题p：f（x）=$\frac{\sqrt{2}}{2}$cos（2x+$\frac{π}{4}$）+sin2x+a，x∈R，3≤f（x）≤6恒成立：命题q：g（x）=log3（ax2+ax+1）的定义域为R，若p∨q为真命题，p∧q为假命题，求a的取值范围．
12．若变量x，y满足约束条件$\left\{\begin{array}{l}{2x+3y≥6}\\{x-y≥0}\\{x≤3}\end{array}\right.$，则函数z=2x+y的最大值和最小值分别是（　　）
A．9和6B．6和$\frac{18}{5}$C．9和5D．9和$\frac{18}{5}$
2．已知点F是抛物线y2=2px的焦点，其中p是正常数，点M的坐标为（12，8），点N在抛物线上，且满足$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$，O为坐标原点．
（1）求抛物线的方程；
（2）若AB，CD都是抛物线经过点F的弦，且AB⊥CD，AB的斜率为k，且k＞0，C．A两点在x轴上方，△AFC与△BFD的面积之和为S，求当k变化时S的最小值．
9．圆x2+y2-2x+4y+3=0的圆心坐标为（　　）
A．（-1，2）B．（1，-2）C．（-2，4）D．（2，-4）
6．把函数y=2sin（2x+$\frac{π}{4}$）的图象向右平移$\frac{π}{8}$个单位，再把所得图象上各点的横坐标扩大为原来的2倍，则所得的函数的解析式是（　　）
A．y=2sin（x+$\frac{3π}{8}$）B．y=2sin（x+$\frac{π}{8}$）C．y=2sinxD．y=2sin4x
7．已知关于x的一元二次方程x2-2（a-2）x-b2+12=0．
（1）若a，b是一枚正方形的骰子（骰子六个面上分别标以数字1，2，3，4，5，6）掷两次所得到的点数，求方程有两正根的概率；
（2）若a∈[2，6]，b∈[0，4]，求方程有实根的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网