题目内容
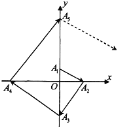
【题目】如图所示,点列![]() 满足:
满足:![]() ,
,![]() ,
,![]() 均在坐标轴上
均在坐标轴上![]() ,则向量
,则向量![]() ()
()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
由于点列{An}满足:|![]() |=1,|
|=1,|![]() |=2|
|=2|![]() |+1,设
|+1,设![]() ,则a1=1,an+1=2an+1,变形为an+1+1=2(an+1),可知;数列{an+1}是等比数列,利用通项公式可得
,则a1=1,an+1=2an+1,变形为an+1+1=2(an+1),可知;数列{an+1}是等比数列,利用通项公式可得![]() .由于Ai均在坐标轴上(i∈N*),且A4n﹣3,A4n﹣2,A4n﹣1,A4n,(n∈N*)分别在y轴的正半轴,x轴的正半轴,y轴的负半轴,x轴的负半轴.
.由于Ai均在坐标轴上(i∈N*),且A4n﹣3,A4n﹣2,A4n﹣1,A4n,(n∈N*)分别在y轴的正半轴,x轴的正半轴,y轴的负半轴,x轴的负半轴.
可得向量![]() 的横坐标=a2﹣a4+a6﹣a8+…+a2010﹣a2012+a2014,向量
的横坐标=a2﹣a4+a6﹣a8+…+a2010﹣a2012+a2014,向量![]() 的纵坐标=a1﹣a3+a5﹣a7+…+﹣a2011+a2013,再利用等比数列的前n项和公式即可得出.
的纵坐标=a1﹣a3+a5﹣a7+…+﹣a2011+a2013,再利用等比数列的前n项和公式即可得出.
∵点列{An}满足:|![]() |=1,|
|=1,|![]() |=2|
|=2|![]() |+1,
|+1,
设![]() ,则a1=1,an+1=2an+1,化为an+1+1=2(an+1),
,则a1=1,an+1=2an+1,化为an+1+1=2(an+1),
∴数列{an+1}是等比数列,
∴![]() 2n.
2n.
∴![]() .
.
由于Ai均在坐标轴上(i∈N*),
且A4n﹣3,A4n﹣2,A4n﹣1,A4n,分别在y轴的正半轴,x轴的正半轴,y轴的负半轴,x轴的负半轴.
∴向量![]() 的横坐标=a2﹣a4+a6﹣a8+…+a2010﹣a2012+a2014
的横坐标=a2﹣a4+a6﹣a8+…+a2010﹣a2012+a2014
=(22﹣1)﹣(24﹣1)+(26﹣1)﹣(28﹣1)+…+(22010﹣1)﹣(22012﹣1)+(22014﹣1)
=22﹣24+26﹣28+…+22010﹣22012+22014﹣1
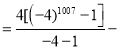 1
1
![]() .
.
同理可得向量![]() 的纵坐标=a1﹣a3+a5﹣a7+…+﹣a2011+a2013
的纵坐标=a1﹣a3+a5﹣a7+…+﹣a2011+a2013![]() .
.
∴向量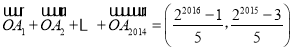 .
.
故选:D.

【题目】党的十九大报告指出,要推进绿色发展,倡导“简约知适度、绿色低碳”的生活方式,开展创建“低碳生活,绿色出行”等行动.在这一号召下,越来越多的人秉承“能走不骑,能骑不坐,能坐不开”的出行理念,尽可能采取乘坐公交车骑自行车或步行等方式出行,减少交通拥堵,共建清洁、畅通高效的城市生活环境.某市环保机构随机抽查统计了该市部分成年市民某月骑车次数,统计如下:
人数 年龄 |
|
|
|
|
|
|
18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
60岁及以上 | 25 | 10 | 10 | 19 | 4 | 2 |
联合国世界卫生组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.
(I)若从被抽查的该月骑车次数在![]() 的老年人中随机选出两名幸运者给予奖励,求其中一名幸运者该月骑车次数在
的老年人中随机选出两名幸运者给予奖励,求其中一名幸运者该月骑车次数在![]() 之间,另一名幸运者该月骑车次数在
之间,另一名幸运者该月骑车次数在![]() 之间的概率;
之间的概率;
(Ⅱ)用样本估计总体的思想,解决如下问题:
(![]() )估计该市在32岁至44岁年龄段的一个青年人每月骑车的平均次数;
)估计该市在32岁至44岁年龄段的一个青年人每月骑车的平均次数;
(![]() ) 若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
) 若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【题目】一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表:
温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵个数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
(I)根据散点图判断,![]() 与
与![]() 哪一个适宜作为产卵数
哪一个适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)红铃虫是棉区危害较重的害虫,可从农业、物理和化学三个方面进行防治,其中农业方面防治有3种方法,物理方面防治有1种方法,化学方面防治3种方法,现从7种方法中选3种方法进行综合防治(即3种方法不能全部来自同一方面,至少来自两个方面),X表示在综合防治中农业方面的防治方法的种数,求X的分布列及数学期望E(X).
附:可能用到的公式及数据表中(表中![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() )
)
|
|
|
|
|
|
|
27.430 | 3.612 | 81.290 | 147.700 | 2763.764 | 705.592 | 40.180 |
对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()


