题目内容
已知函数
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)确定函数 在
在 上的单调性并求在此区间上
上的单调性并求在此区间上 的最小值.
的最小值.

(Ⅰ)求函数
 的最小正周期;
的最小正周期;(Ⅱ)确定函数
 在
在 上的单调性并求在此区间上
上的单调性并求在此区间上 的最小值.
的最小值. (Ⅰ) ;(Ⅱ)
;(Ⅱ)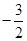 .
.
 ;(Ⅱ)
;(Ⅱ)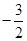 .
.试题分析:(Ⅰ)先由二倍角公式对函数
 降次,然后利用三角恒等变换化为
降次,然后利用三角恒等变换化为 的形式,从而可以求出最小正周期;(Ⅱ)由上问易知,函数的单调递增区间是
的形式,从而可以求出最小正周期;(Ⅱ)由上问易知,函数的单调递增区间是 ,
, ;单调递减区间是
;单调递减区间是 .所以函数
.所以函数 在
在 上单调递增,在
上单调递增,在 上单调递减.再通过比较
上单调递减.再通过比较 而得函数
而得函数 在
在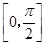 上的最小值是
上的最小值是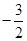 .
.试题解析:(Ⅰ) 依题意
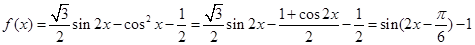 ,
,则
 的最小正周期是
的最小正周期是 ; 4分
; 4分(Ⅱ)
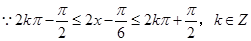 .
. .
.所以函数的单调递增区间是
 ,
, ;单调递减区间是
;单调递减区间是 .
.所以函数
 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减又
 所以函数
所以函数 在
在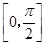 上的最小值是
上的最小值是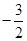 .
.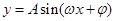 的图像和性质.
的图像和性质.
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,下列命题:
,下列命题: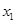 ,
, ,当
,当 时,
时, 成立;
成立; 在区间
在区间 上是单调递增;
上是单调递增; 成中心对称图像;
成中心对称图像; 个单位后将与
个单位后将与 的图像重合.
的图像重合. 的部分图像如图,则
的部分图像如图,则 ( )
( )


 的一段图象如图所示.
的一段图象如图所示.
 的解析式;
的解析式; 求函数
求函数 的单调递增区间.
的单调递增区间. 的图象过点(0,
的图象过点(0,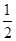 ),最小正周期为
),最小正周期为 ,且最小值为-1.
,且最小值为-1. 的解析式.
的解析式. ,
, ,求m的取值范围.
,求m的取值范围.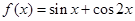 的图象为( )
的图象为( )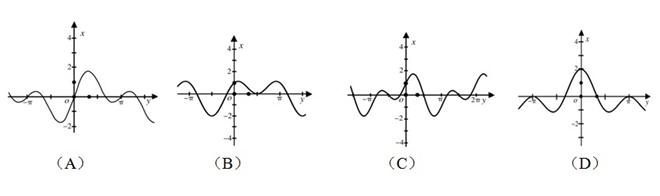
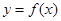 的图象上每一点的纵坐标保持不变,横坐标缩小到原来的
的图象上每一点的纵坐标保持不变,横坐标缩小到原来的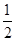 ,再将整个图象向右平移
,再将整个图象向右平移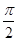 个单位,沿
个单位,沿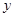 轴向下平移
轴向下平移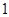 个单位,得到函数
个单位,得到函数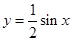 的图象,则函数
的图象,则函数



 ,下面结论错误的是( )
,下面结论错误的是( ) 的最小正周期为
的最小正周期为
 对称
对称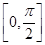 上是增函数
上是增函数 ,x∈R,若
,x∈R,若 ≥1,则x的取值范围为
≥1,则x的取值范围为


